The Mellor Yamada Level 2.5 Turbulence Closure Model
This mixing model is described in detail in Mellor and Yamada (1982) and in the Princeton Ocean Model Users Guide (Mellor, 1998). To implement MY mixing in HYCOM, viscosity and scalar diffusivity are first parameterized as follows:
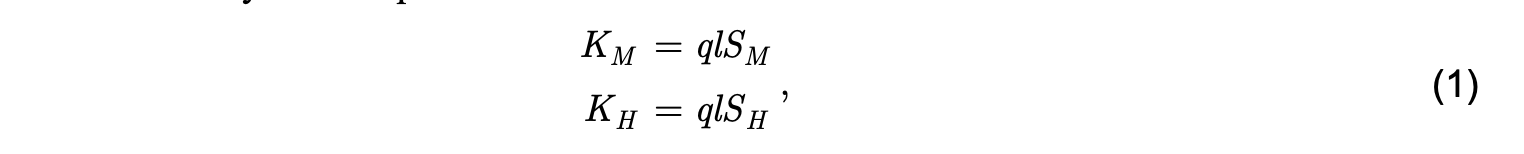
where SM and SH are expressed as
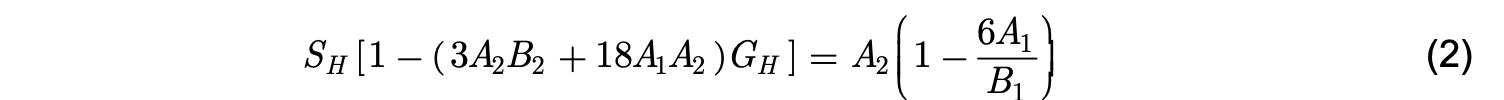
and
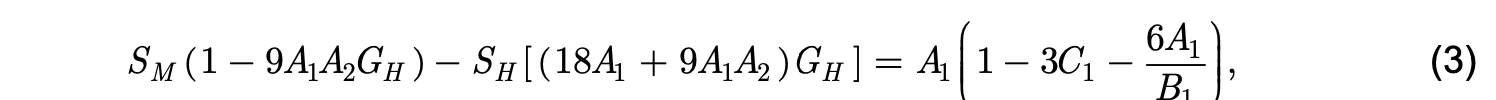
with
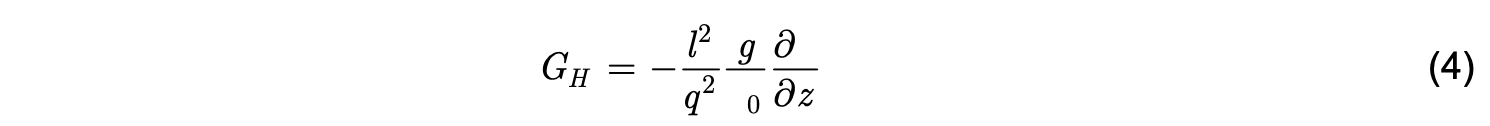
being a Richardson number. In these expressions, q is the turbulence velocity scale, l is the turbulence length scale, and r is the potential density. The variables q2 (turbulent kinetic energy) and q2l are prognostic variables in this model. The equations for these variables, written here as a function of the generalized vertical coordinate s for the purpose of HYCOM implementation, are
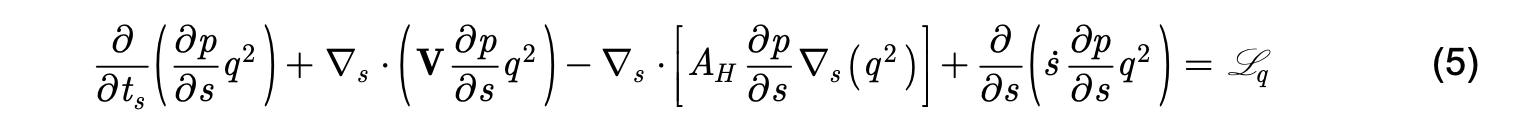
and
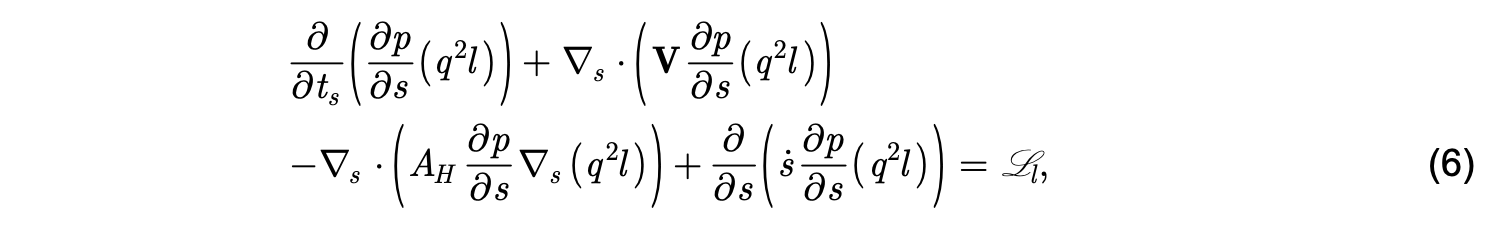
where Lq and Ll represent the sum of all local processes. Equations (5) and (6) have the same form as the equations for T and S in generalized vertical coordinates. Terms two through four in both equations represent horizontal advection, horizontal diffusion, and fluxes across the generalized vertical coordinates when these coordinates are relocated (s≠0) by the hybrid coordinate adjustment algorithm. For T and S, the local processes are surface forcing and vertical diffusivity. For q2 and q2l , the local processes are boundary forcing and vertical diffusivity plus three additional forcing and damping mechanisms described in the following section.
The strategy for implementing this turbulence closure model in HYCOM is to solve the same local equations for q2 and q2l that are solved in POM. The purely local equations are
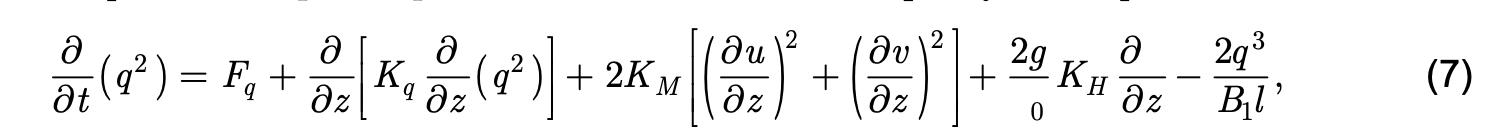
and
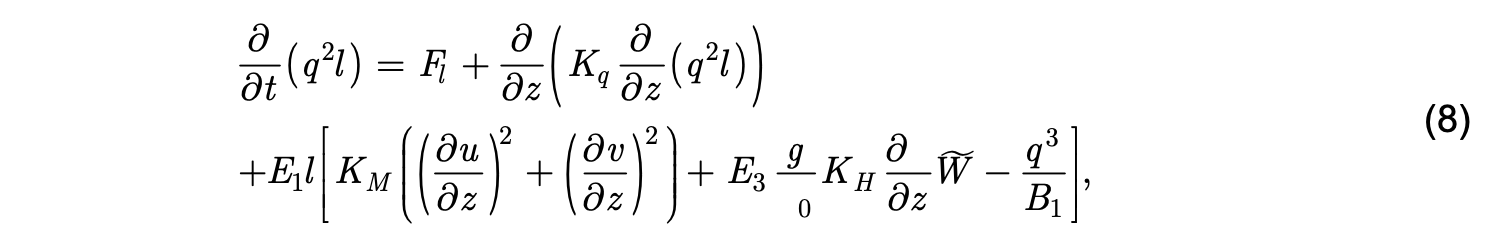
where Fq and Fl represent local boundary forcing and the remaining four terms of each equation represent vertical diffusion, generation by vertical shear, conversion to and from potential energy, and dissipation. The parameter ˜W is the wall proximity function given by ˜W = 1 + E2(l+kL), with L-1 = (h-z)-1 +(H-z)-1, where h is sea surface elevation and H is water depth. The local solution procedure implemented in HYCOM is essentially the same one used in POM. Values of the several constants used in HYCOM are the same as those used in POM (see Mellor, 1998).
Existing HYCOM algorithms are employed to calculate changes in q2l and q2l due to the two nonlocal terms and the s& term in (5) and (6). Horizontal advection and diffusion of q2 and q2l are performed in subroutine tsadvc.f, while the s& flux terms are estimated in the hybrid vertical coordinate subroutine hybgen.f. Both q2 and q2l are carried at the two leap frog time steps, and time smoothing is performed in the same manner as for other model layer variables.
One significant problem had to be overcome to implement the algorithm in this manner. In the POM Mellor-Yamada algorithm, the variables q2 and q2l are carried at vertical interfaces while HYCOM scalars are carried as layer variables. The strategy employed is to define a separate vertical coordinate system on which the one-dimensional solutions for q2 and q2l are performed. This MY vertical coordinate system is illustrated alongside the HYCOM vertical coordinate system in the Figure. MY interfaces are located at the central depths of HYCOM model layers. There is one additional layer and one additional interface present in the MY coordinate system. With q2 and q2l defined on MY interfaces, implementation of the POM local solution procedure in HYCOM is straightforward. Since MY interfaces are located at the central depths of HYCOM layers, values on MY interfaces are passed to the HYCOM routines that calculate the horizontal advection, horizontal diffusion, and s& flux terms of (5) and (6). After these algorithms are executed, the layer values of q2 and q2l are passed as interface values on the MY grid to the one-dimensional solution algorithm. When the one-dimensional routine is executed, HYCOM momentum and thermodynamical layer variables must be vertically interpolated to the MY layers. Since the central depth of each MY layer is located half way between the central depths of two HYCOM layers, the interpolated MY layer variables are calculated as the average values of these two HYCOM layers.
Instead of employing the POM procedures to solve vertical diffusion equations for other model variables, the procedure used for the KPP mixing algorithm is employed in HYCOM. Specifically, the vertical viscosity and scalar diffusivity profiles from (1) obtained from the local solutions of (7) and (8) are used in the tridiagonal matrix algorithm described in Appendix C.
Mellor, G. L., 1998: Users Guide for a Three-Dimensional, Primitive Equation Numerical Ocean Model. Available on the Princeton Ocean Model web site.
Mellor, G. L. and Yamada, T., 1982: Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys., 20, 851-875.
