Hybrid Coordinate Adjustment Algorithm
Bleck (2002) describes the hybrid vertical coordinate grid generator along with its initial implementation in a global version of HYCOM. The following description also describes the substantial modification to this algorithm that has occurred since then.
The algorithm controlling the transition between isopycnic and level (p) coordinates in the open ocean works as follows: Consider three consecutive isopycnic layers labeled 0, 1, and 2 in a stratified water column where the user has set the minimum thicknesses to d0, d1, and d2, respectively. Suppose that specific volume α1 differs from its isopycnic reference value α̂1 . To restore isopycnic conditions, it is necessary to re-discretize the water column in a manner that preserves the overall height of the column, represented by the integral ∫αdp, while changing α1 to α̂1. Conservation of the integral requires that one or more layer interfaces must be relocated to different pressure levels. If layer 1 is too dense (α1 < α̂1), the upper interface is moved upward to μ transfer less-dense water from layer 0 to layer 1. If layer 1 is too light (α1 > α̂1), the lower interface is moved downward to transfer denser water from layer 2 to layer 1. This method does not work for the model layer in contact with the bottom if it is too light. A special algorithm described below is included to handle this case by extruding water into the layer above.
The two cases α1 < α̂1 and α1 > α̂1 are discussed separately. For the first case where the layer is too dense (α1 < α̂1), the upper interface is moved upward and mass is exchanged between layers 0 and 1. Conservation of ∫αdp requires that the upper interface be moved to the new pressure interface
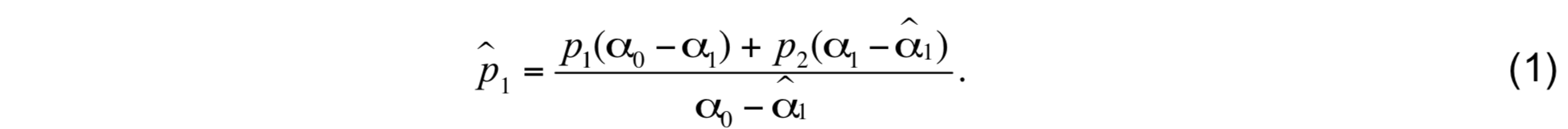
Since the weight assigned to p2 is negative, (1) will not necessarily yield a solution p̂1 > p0 for large differences between α1 and α̂1 . This is no problem because the minimum thickness constraint is applied to layer 0 by replacing p̂1 by
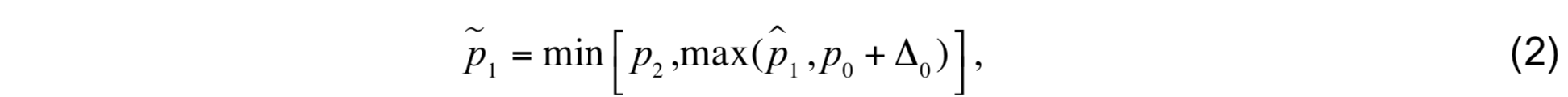
where ∆0 is a specified minimum layer thickness. Of course, moving the interface to ˜p instead of p̂ no longer permits isopycnic conditions to be restored.
Following Bleck and Benjamin (1993), the user chooses the absolute minimum thickness δ0. The actual minimum thickness ∆0 is then calculated in a manner that insures a smooth transition between the isopycnic and non-isopycnic domains. The function ∆0 is determined by a μ continuously differentiable “cushion” function, which for large positive arguments ∆p ≡ p̂1 − p0 returns the argument ∆p (meaning that ˜p1 = p̂1) and for large negative arguments returns δ0:
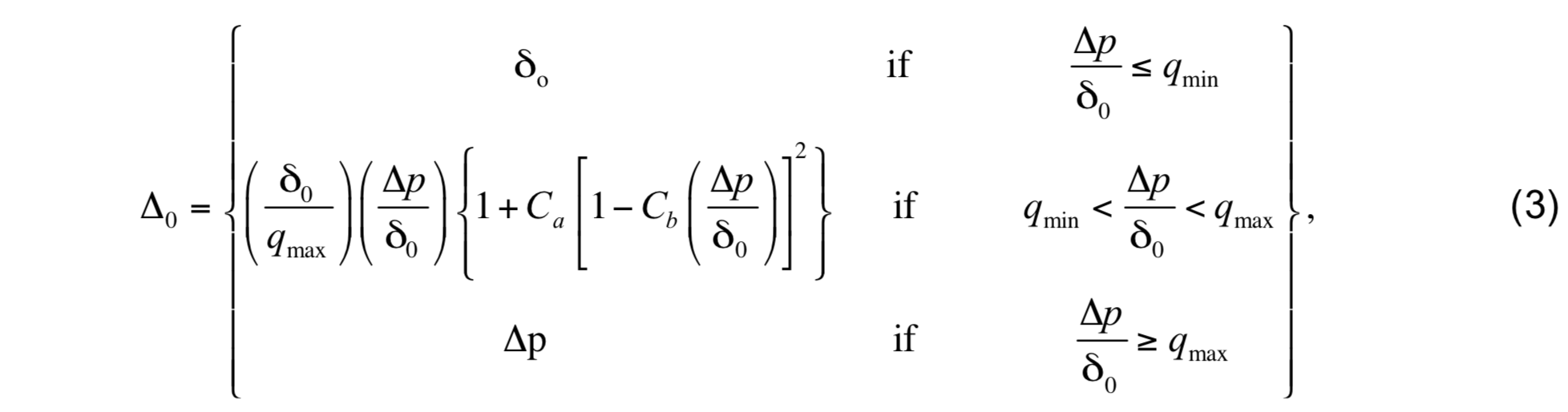
where the constants are given by
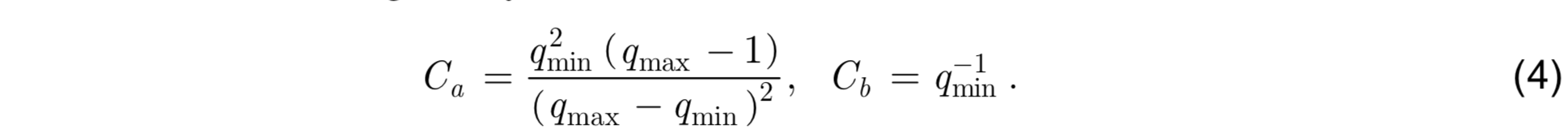
The limits qmin and qmax control the width of the transition zone between isopycnic and z coordinates, and are set to default values of qmin = -2 and qmax = 4. When the upper interface must be raised, lighter water is entrained to increase α1 to a value ˜α1:
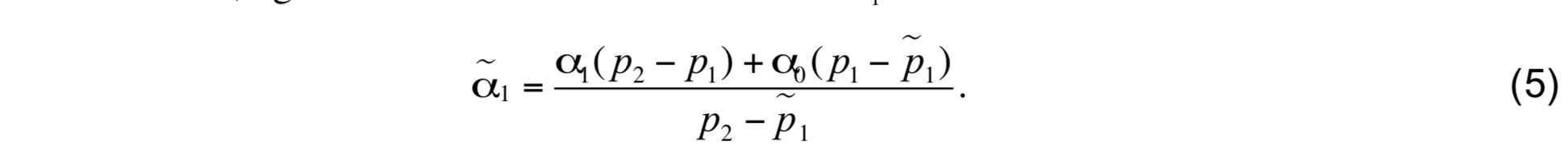
However, application of the minimum thickness requirement can make it necessary for the upper interface to be lowered (˜p1 > p1) and thus modify layer 0. Conservation of ∫α_dp_ then leads to
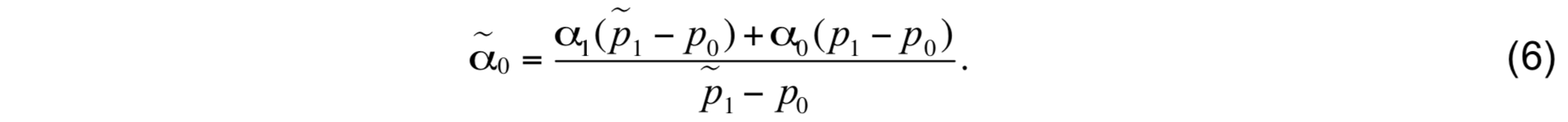
The preservation of minimum layer thickness by increasing the thickness of layer 0 always overrides attempts to restore isopycnic conditions.
For the second case where layer 1 is too light (α1 > α̂1), the lower interface is moved downward and mass from layer 2 is entrained into layer 1. Conservation of ∫α_dp_ yields the new pressure level to which the interface must be relocated:
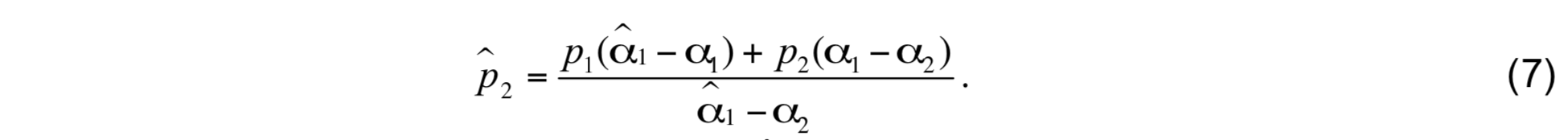
To maintain the minimum thickness of layer 2p̂2 is replaced by
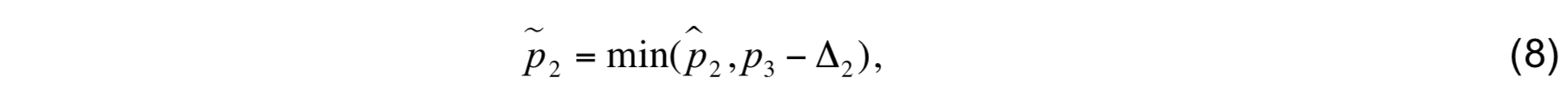
where ∆2 is determined from the cushion function
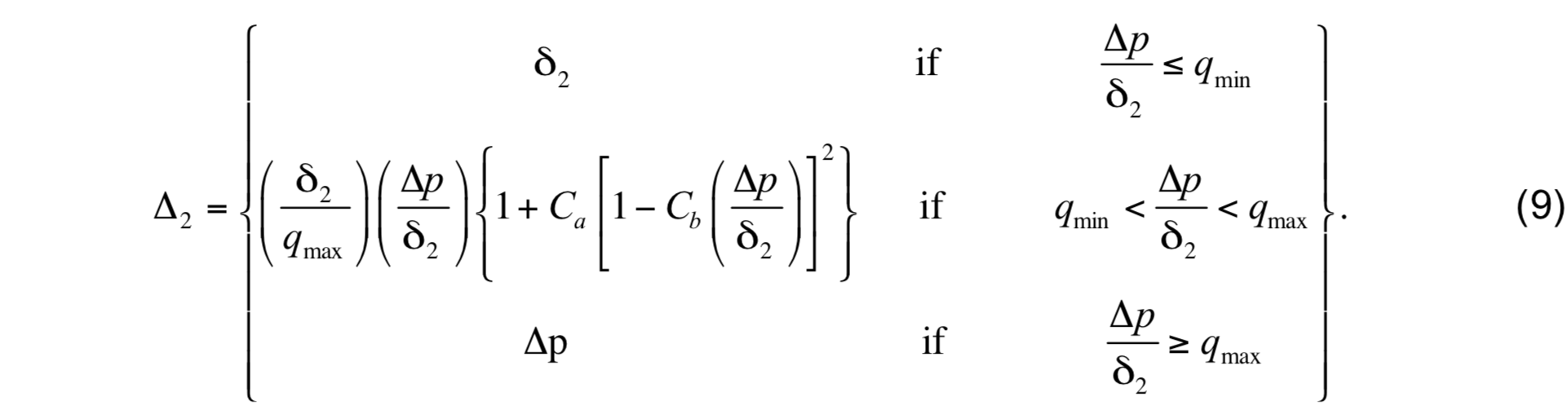
with ∆p ≡ p3 − p&770;2. The following additional limitations are imposed on ˜p2:
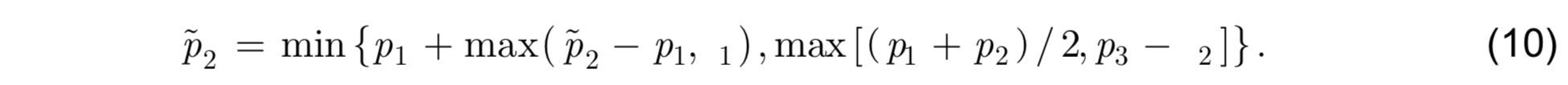
If layer 1 is the deepest layer with nonzero thickness and it is too light, interface 2 cannot move downward to restore isopycnic conditions and a special algorithm must be executed: Since only interface 1 can be moved, this interface is moved downward to restore isopycnic conditions in layer 1. An “unmixing” algorithm is employed to achieve this goal. The water in layer 1 must be restratified into two sublayers such that the density of the upper sublayer exactly equals the density of layer 0, the density of the lower sublayer is close to the desired reference density, and the density averaged over the two sublayers equals the original layer density. Given
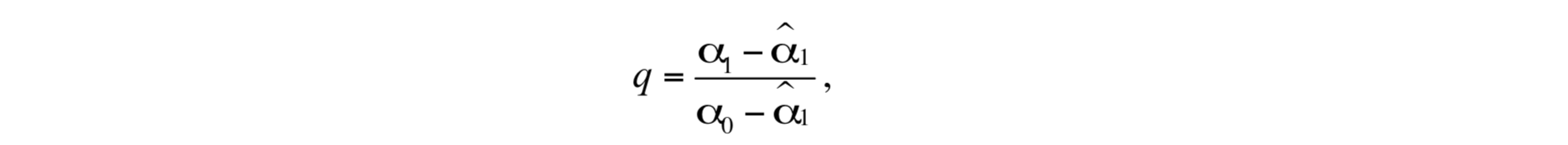
interface 1 is relocated using
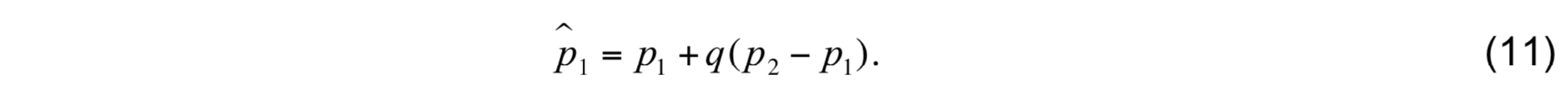
Thermodynamical variables in the lower sublayer are then calculated using
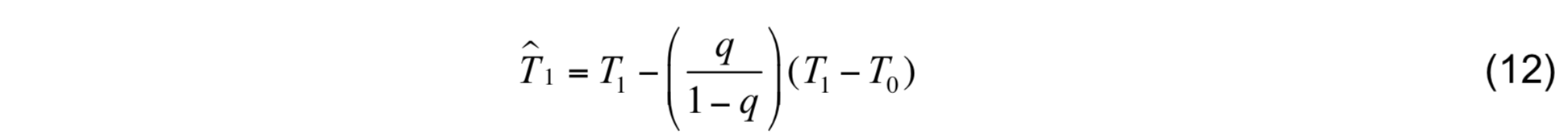
for T, and the same equation for S and a. (Actually, two of the thermodynamical variables are diagnosed using (12) with the third estimated from the equation of state). The closeness of lower sublayer density to the reference density is sacrificed if necessary to achieve two goals: (1) to prevent the thickness of layer 1 from decreasing by more than 50% using
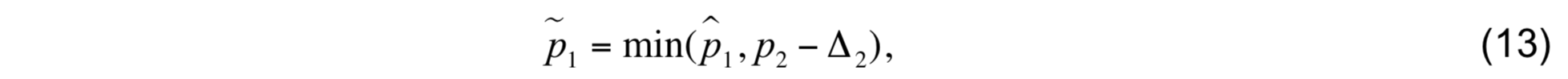
where ∆2 = (p2 − p1)/2, and (2) to prevent runaway changes in T and S using
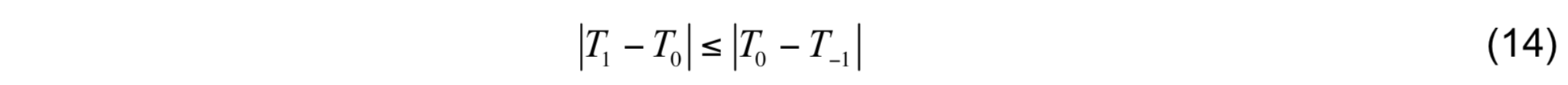
for T and the analogous equation for S.
In practice, if T and S are fluxed across the relocated interfaces, then perfect restoration of isopycnic conditions is not possible (˜a1 ≠ â1) due to the nonlinear equation of state. For this reason, HYCOM allows the user to choose which two of the three thermodynamical variables T, S, and a are fluxed across the moving interface. In each case, the third variable is calculated using the equation of state. When a is one of the fluxed variables, then cabbeling is not a problem. However, since either T or S are no longer conserved in this case, it is desirable to minimize the negative influence of cabbeling to allow T and S to be fluxed across relocated interfaces. To achieve this, the following iterative procedure is included to insure in most cases that |˜α1 − α̂1| is smaller than a prescribed tolerance after applying the grid generator. The new T value that results from raising the interface is
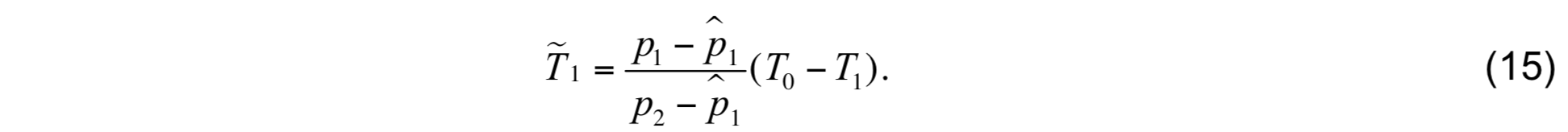
With S1 estimated in the same manner, a new estimate of ˜α is made using the model equation of state. If |˜α1 − α̂1| exceeds the required tolerance, then â1 is recalculated using
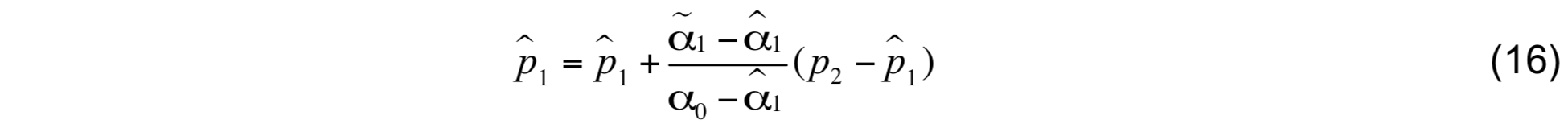
In this step, p̂1 is not permitted to exceed p1. The resulting specific volume ˜α1 is then recalculated, and if the prescribed tolerance is not achieved, then p̂1 is recalculated by the same procedure. The procedure is repeated up to five times if necessary.
Although uncommon, there is a more significant problem that can arise from the nonlinear equation of state when T and S are fluxed across relocated interfaces. During HYCOM development, cabbeling resulting from vertical coordinate adjustment (in conjunction with T and S horizontal advection and diffusion) caused excessive interface relocation in limited regions such as beneath the Mediterranean salt tongue. The nonlinear equation of state can, for certain T, S profiles, produce either insignificant density changes or density changes of the wrong sign within a model layer when the grid generator relocates either the upper or lower interface. Repeated application of the grid generator then produces unacceptably large vertical coordinate migration. Code is therefore included in HYCOM to suppress the vertical coordinate adjustment when the change in α1 does not have the expected sign or when excessive coordinate migration would be necessary to restore isopycnic conditions.
The complete hybrid coordinate adjustment algorithm in HYCOM also includes the transition between the open-ocean p and isopycnic coordinates to sigma coordinates in shallow water and back to p coordinates in very shallow water. This is implemented in a very simple manner. First, the user specifies the number of model layers Ns that are to become sigma coordinates along with the absolute minimum thickness δmin that is permitted for the sigma coordinates. These are specified in addition to the user-specified open-ocean minimum thicknesses dk for layer k. The minimum thickness of the sigma coordinates is constant for all model layers and is given by
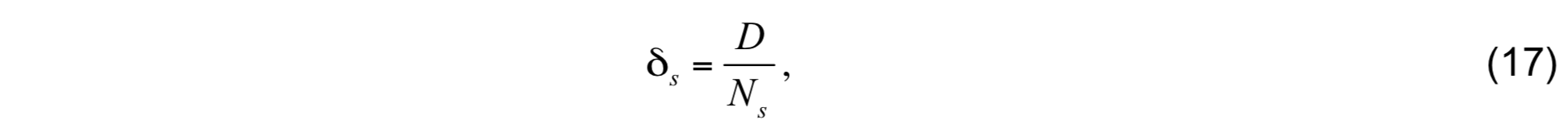
where D is the total water depth.
The full grid generator is then implemented by calculating the following minimum thickness value for each model layer:
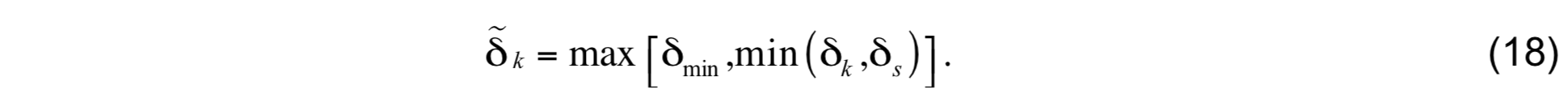
In a given model layer, the transition to sigma coordinates occurs where the water depth becomes sufficiently shallow to make δs < δk. The transition back to level coordinates occurs where the water depth becomes sufficiently shallow to make δs < δmin. Thus, the proper coordinate s min transformation is assured if δk is replaced by δk before executing the vertical coordinate adjustment. Only the upper Ns layers will transition to sigma coordinates. Deeper layers will collapse to zero thickness at the bottom.
When the hybrid grid generator is called, it is executed separately at each grid point. Thermodynamical variables are adjusted first at the pressure grid points. Before adjusting the vertical coordinates, the initial one-dimensional profiles of temperature, salinity, and density, plus the one-dimensional array of interface pressures, are saved. If the primary Kraus-Turner mixed layer model is selected, an unmixing algorithm must be performed so that the thermodynamical adjustments are consistent with this model. The model layer containing the mixed layer base is divided into two sublayers, and the mixed layer base is temporarily considered to be an additional vertical coordinate. Thermodynamical variables in the two sublayers are then estimated using the same “unmixing” algorithm that is used in the KTA model.
Once the profiles are saved, the vertical adjustment of vertical coordinates is performed at the pressure grid points using the previously outlined procedures. The subsequent adjustments of model thermodynamical variables and momentum must conserve their vertically averaged values and, for the thermodynamical variables, restore density as close to the isopycnic reference value as possible. The classic donor cell scheme satisfies these criteria, but has the undesirable property of being directionally dependent. For example, consider a sequence of model interfaces that have been moved downward to increase the density of intervening layers. If variables are mixed across the relocated interfaces from the top down, the mixing that previously occurred in layer k - 1 does not influence the mixing in layer k. If variables are mixed from the bottom up, however, the mixing that previously occurred in layer k + 1 does influence the mixing in layer k.
The algorithm included in HYCOM remaps each variable from the old to the new vertical grid in a manner that satisfies the two conditions mentioned above, but that is not directionally dependent. Given interface pressures pk on the old grid and ˜pk on the adjusted grid, where K is the number of model layers, the old temperature profile is mapped onto the new adjusted vertical coordinates using
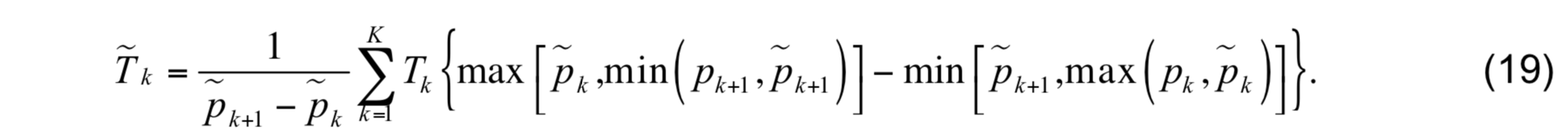
Note that K must be increased by one when the KTA mixed layer model is used to account for the two sublayers within the layer containing the mixed layer base. In practice, the summation is performed between k = k1 to k = k2 in order to eliminate layers on the old vertical grid that do not overlap layers on the new grid. The downside to this procedure occurs in a model layer k if the interface k above is relocated upward and the interface k + 1 below is relocated downward. In this case, the simultaneous mixing across both interfaces will prevent perfect restoration of the isopycnic reference density in layer k. However, repeated application of this procedure will tend to drive the density of layer k toward its reference density. This fact coupled with the absence of directional dependence support our choice of (19) to remap variables on the adjusted grid in lieu of a one-way donor cell scheme.
Donor-cell vertical advection schemes are known to produce numerically induced diffusion. For this reason, the re-mapping scheme has been further modified at the Naval Research Laboratory by A. J. Wallcraft to use the higher-order PLM algorithm within the nearsurface non- isopycnic domain where the distances that interfaces are relocated are relatively large, and numerical diffusion is thus expected to be large. In the isopycnic interior where mixing is very weak, the original remapping algorithm is retained because the PLM algorithm has the undesirable effect of changing values of layer variables within a layer when fluid is only detrained from that layer. Tests have validated that this undesirable effect is outweighed by the positive effect of numerical diffusion reduction.
After adjusting the thermodynamical variables at pressure grid points, the momentum components are then adjusted on the u, v grid points in a manner that conserves vertically averaged momentum. The old and new vertical coordinates obtained at pressure grid points are first interpolated to the u grid points. The adjustment of u is then performed using an equation of the form (19). The same procedure is used to update v at the v grid points.
Bleck, R., 2002: An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Modelling, 4, 55-88.
Bleck, R. and S. Benjamin, 1993: Regional weather prediction with a model combining terrain- following and isentropic coordinates, Part 1: Model description. Mon. Wea. Rev., 121, 1770-1785.