The Simplified Kraus Turner Mixed Layer Model for Hybrid Coordinates (KTB)
The simplified Kraus-Turner slab mixed layer model (KTB) does not carry the mixed layer thickness as a full prognostic variable, in contrast to model KTA. Bleck (2002) used the KTB model in his initial global simulation using HYCOM. The tradeoff between using KTA and KTB is between improved computational efficiency and reduced accuracy. Since the KTA model is far from perfect, this simplified model is adequate for many purposes. Kraus-Turner mixed layer models compute the change of mixed layer thickness over a small time interval ∆t . They require the old mixed layer information, which can be viewed as the cumulative result of past applications of the Kraus-Turner algorithm, as the initial condition. The KTB model contains a simple diagnostic procedure to find the new depth of the mixed layer base to avoid the necessity of unmixing, and to avoid the ambiguities of constructing a representative mixed layer velocity field to advect the mixed layer base (which as a material variable needs to follow the flow).
Beginning at the top of the water column (layer 1), the algorithm searches for the first layer k whose density exceeds the average density ρ of the overlying layers combined (layers 1 through k−1). This layer is assumed to contain the mixed layer base. Layer k is divided into sublayers with different densities. The density ρup of the upper sublayer is set equal to ρ while the density ρlo of the lower sublayer is assigned a value within the range ( ρk + ρk+1 ) , for example ρlo = ( ρk + ρk+1 ) / 2 . Density conservation during sublayer formation yields the depth of the interface separating the sublayers, which is taken to be the mixed layer depth. This pressure interface is given by
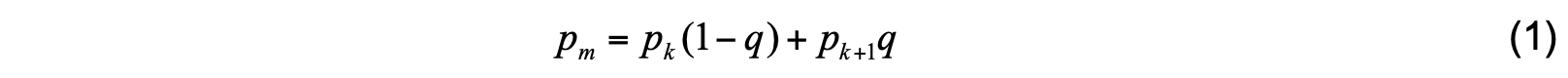
where pk, pk+1 are the upper and lower interface pressures of layer k, and
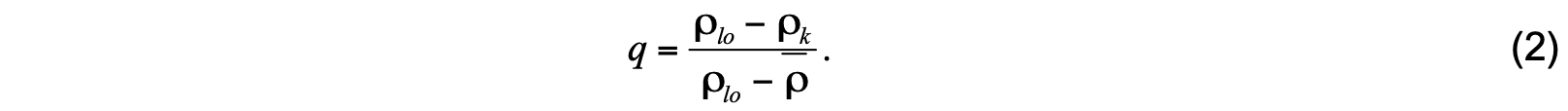
Assignment of temperature/salinity values for the depth interval (0, pk+1) follows the above philosophy of assuming homogeneity between the surface and pm . With the mixed layer depth already determined by (1), lower sublayer values of temperature and salinity follow from the requirement that their column integrals be invariant during the redistribution process. Specifically, we set Tup = T̅ and Sup = S̅ , where the overbar again indicates the average over layers k through k−1. The lower sublayer values become
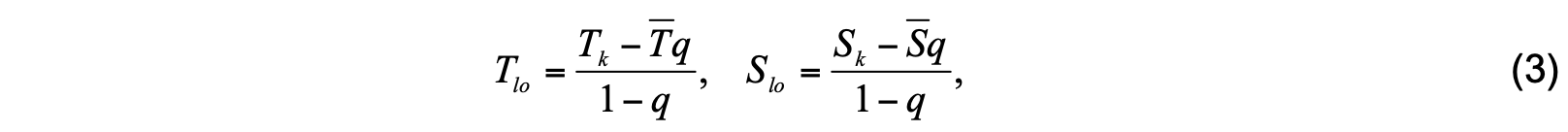
with q defined by (2).
Given the nonlinear nature of the equation of state, the upper and lower sublayer densities must be recomputed after temperature and salinity have been homogenized over layers 1 through k−1 and unmixed in layer k . After this, the density profile, characterized by homogeneous conditions between the surface and pressure pm and a density discontinuity at that pressure, is provided to the K-T TKE algorithm to calculate the new mixed layer depth. Temperature and salinity are homogenized over the new mixed layer depth, and the surface fluxes are distributed over the same depth range. The resulting temperature and salinity profiles are then projected back onto the original hybrid coordinate profile. The sublayer information is not saved.
It is important to note that the sublayer formation and deletion cycle by itself does not cause a drift in the T / S profile provided that layers 1 through k−1 are fully homogenized to begin with. In other words, the original T / S profile is recovered if ∆t → 0 . Initial experiments with this scheme indicate that best results are obtained by assigning ρlo a value closer to ρk than to
ρk+1 . To skip the necessity of forming sublayers, set ρlo = ρk (i.e., q = 0 ). The T / S profile transmitted to the K-T TKE algorithm in this case is obtained from the original profile by homogenizing temperature and salinity down to depth pk and setting pm = pk.
Bleck, R., 2002: An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Modelling, 4, 55-88.