KPP Vertical Mixing

KPP Vertical Mixing

1. Diapycnal Diffusivity in the Ocean Interior

     The K-Profile Parameterization (KPP) model is described in detail in Large et al. (1994). To summarize the implementation of KPP mixing in HYCOM, model variables are first decomposed into mean (denoted by an overbar) and turbulent (denoted by a prime) components. Diapycnal diffusivities and viscosity parameterized in the ocean interior as follows:

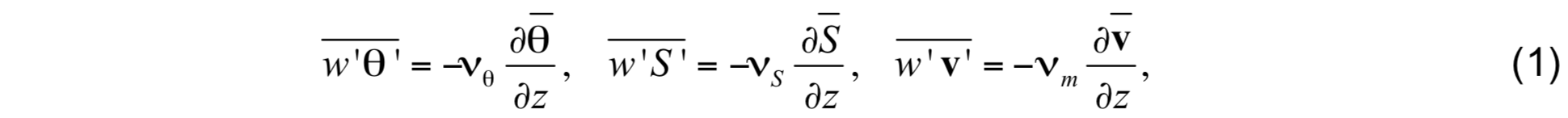
where ν_θ, ν_S, ν_m are the interior diffusivities of potential temperature, salinity (which includes other scalars), and momentum (viscosity), respectively. Interior diffusivity/viscosity is assumed to consist of three components, which is illustrated here for potential temperature:

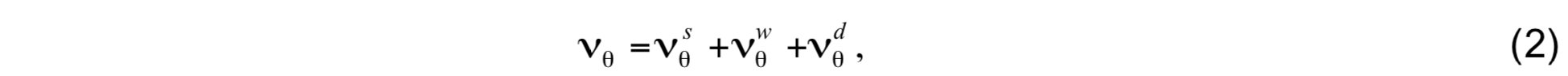
where ν_θ^S is the contribution of resolved shear instability, ν_θ^w is the contribution of unresolved shear instability due to the background internal wave field, and ν_θ ^d is the contribution of double diffusion. Only the first two processes contribute to viscosity.

     The contribution of shear instability is parameterized in terms of the gradient Richardson number calculated at model interfaces:

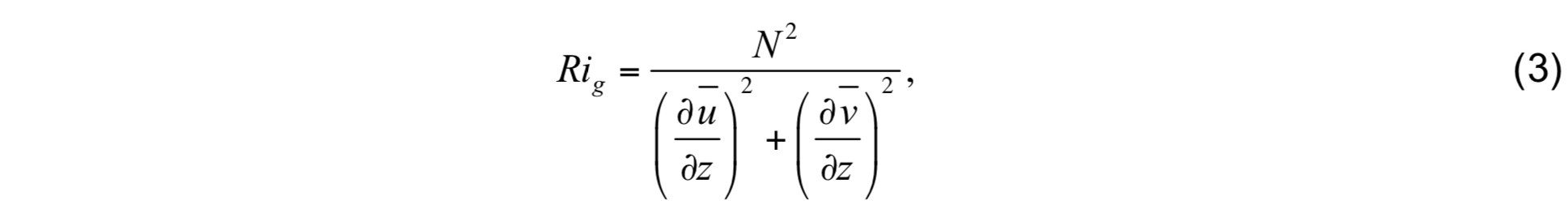
where mixing is triggered when Ri_g = Ri₀ < 0.7. Vertical derivatives are estimated at model interfaces as follows: Given model layer k bounded by interfaces k and k + 1, the vertical derivative of u̅ at interface k is estimated as

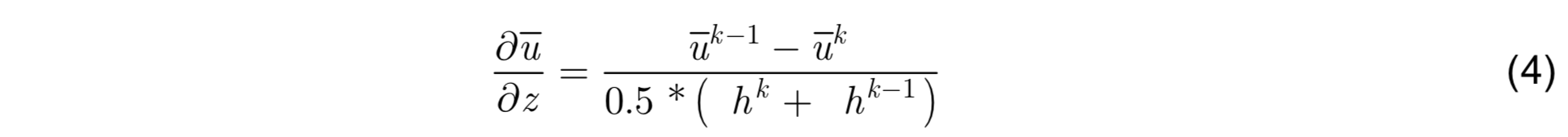
where the denominator contains the thickness of layers k and k - 1. The contribution of shear instability is the same for θ diffusivity, S diffusivity, and viscosity (ν^s = ν^s_θ = ν^s_S = ν^s_m), and is given by

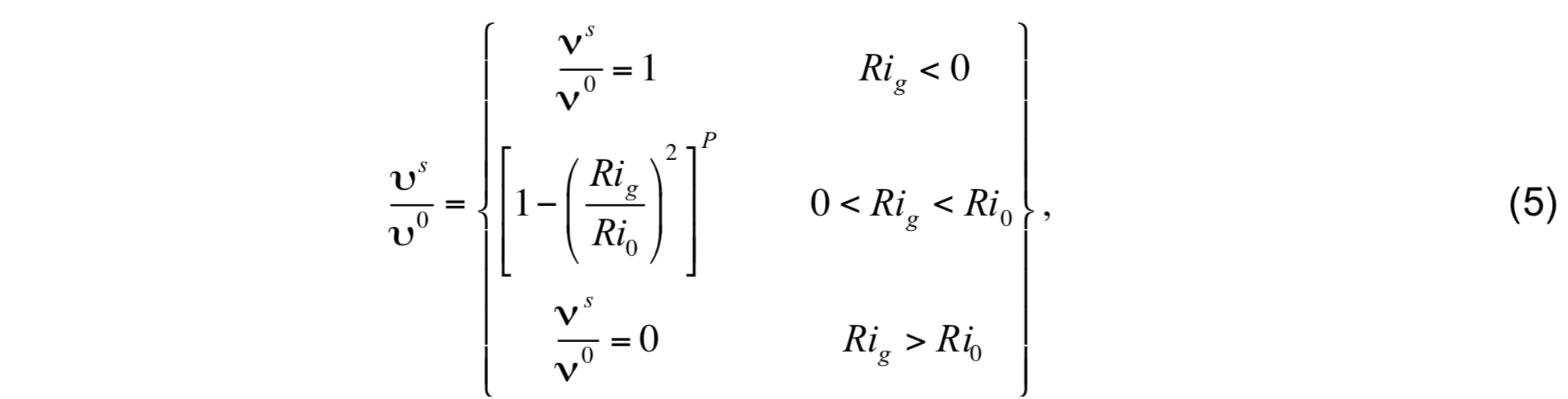
where ν⁰ = 50 × 10⁻⁴m²s^-1, Ri₀ = 0.7, and P = 3.

     The diffusivity that results from unresolved background internal wave shear is given by

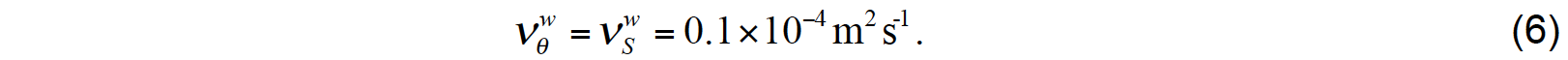
Based on the analysis of Peters et al. (1988), Large et al. (1994) determined that viscosity should be an order of magnitude larger:

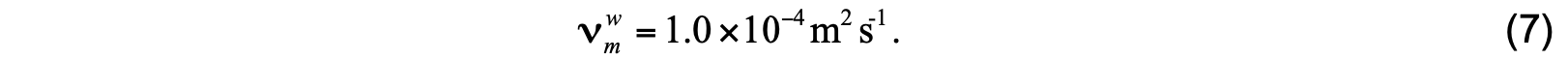
Regions where double diffusive processes are important are identified using the double diffusion density ratio calculated at model interfaces:

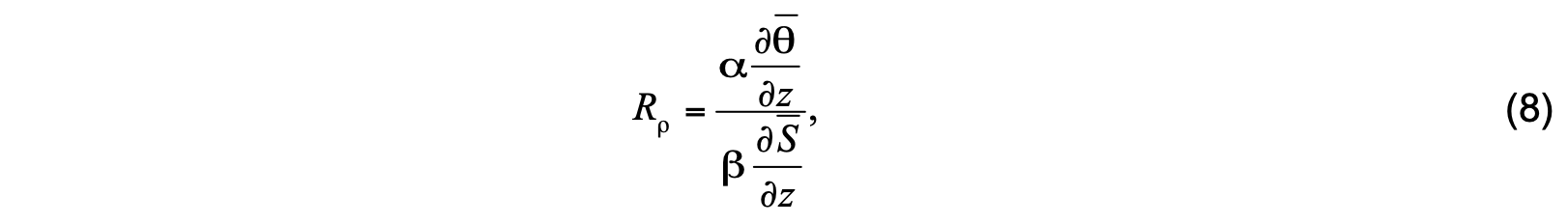
where α and β are the thermodynamic expansion coefficients for temperature and salinity, respectively. For salt fingering (warm, salty water overlying cold, fresh water), salinity/scalar diffusivity is given by

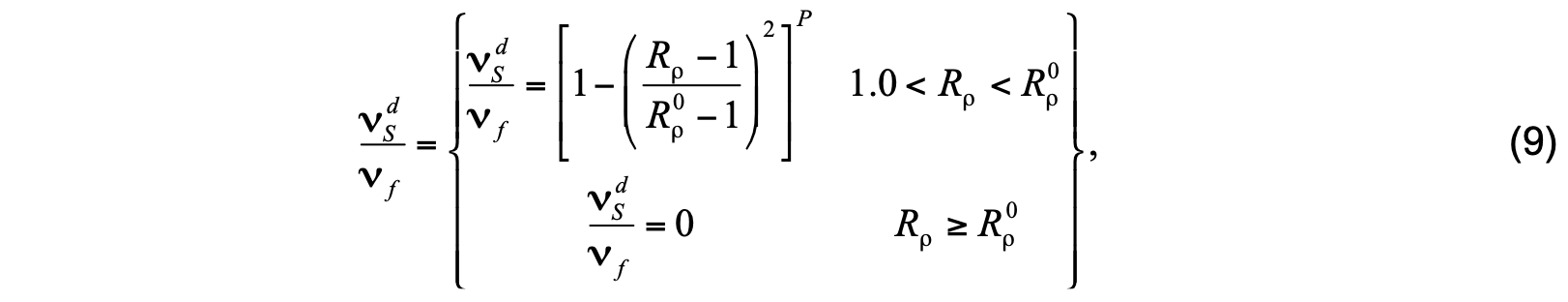
and temperature diffusivity is given by

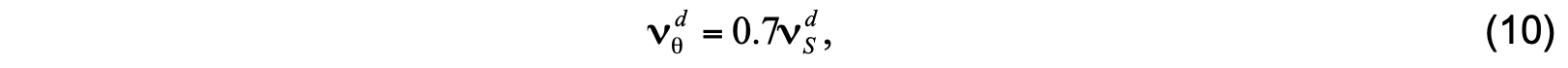
where ν_f = 10×10⁻⁴m²s^-1, R₀ = 1.9,and P= 3. Fordiffusiveconvection,temperature diffusivity is given by

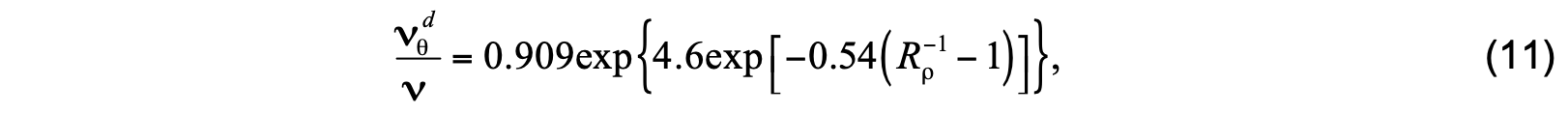
where ν is the molecular viscosity for temperature, while salinity/scalar diffusivity is given by

2. Diagnosis of the Surface Boundary Layer Thickness

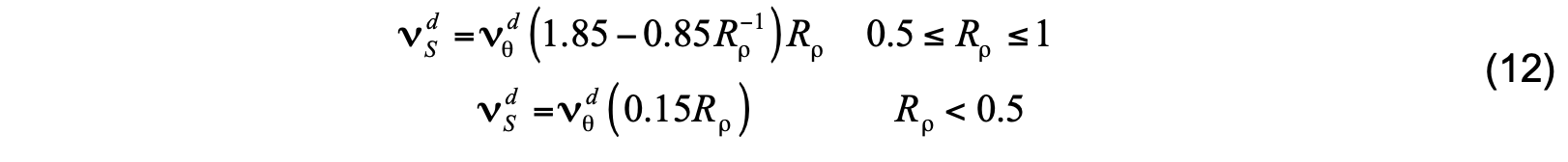
      The diagnosis of h_b is based on the bulk Richardson number

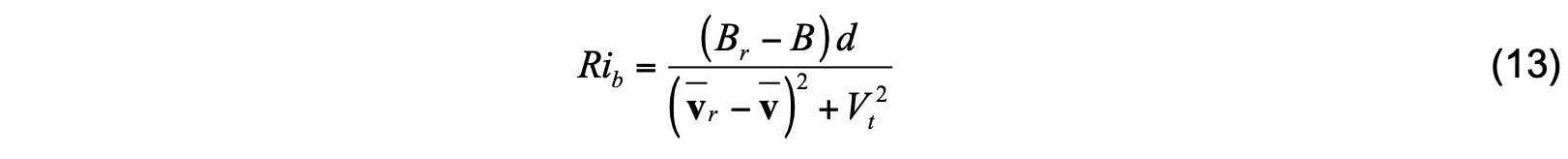
where B is buoyancy, d is depth, the subscript r denotes reference values, and where the two terms in the denominator represent the influence of resolved vertical shear and unresolved turbulent velocity shear, respectively. Reference values are averaged over the depth range εd, where ε = 0.1. At depth d = h_b , the reference depth h_b represents the thickness of the surface layer where Monin-Obukhov similarity theory applies. In practice, if model layer 1 is more than 7.5m thick, reference values in (13) are set to those of layer one. Otherwise, averaging is performed over the depth range εd.
      The surface boundary layer thickness (which is distinct from mixed layer thickness) is the depth range over which turbulent boundary layer eddies can penetrate before becoming stable relative to the local buoyancy and velocity. It is estimated as the minimum depth at which Ri_b exceeds the critical value Ri_c = 0.3. The Richardson number Ri_b is estimated in (13) as a layer variable, and thus assumed to represent the Richardson number at the middle depth of each layer. Moving downward from the surface, Ri_b is calculated for each layer. When the first layer is reached where Ri_b > 0.3 , h_b is estimated by linear interpolation between the central depths of that layer and the layer above.
      The unresolved turbulent velocity shear in the denominator of (13) is estimated from

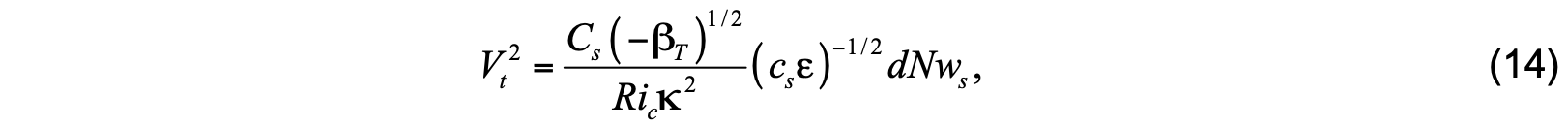
where C_s is a constant between 1 and 2, β_T is the ratio of entrainment buoyancy flux to surface buoyancy flux, κ = 0.4 is the von Karman constant, and w_s is the salinity/scalar turbulent velocity scale. The latter scale is estimated using

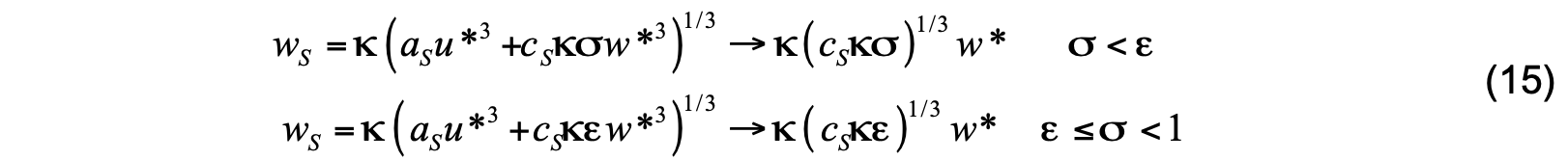
where a_x and c_x are constants, w^* = ( −B_f / h )^1/3 is the convective velocity scale with B_f being the surface buoyancy flux, and σ = d / h_b . Expressions to the right of the arrows represent the convective limit. In HYCOM, w_s values are stored in a two-dimensional lookup table as functions of u^*3 and σ w^*3 to reduce calculations. If the surface forcing is stabilizing, the diagnosed value of h_b is required to be smaller than both the Ekman length scale h_E = 0.7 u^* / f and the Monin-Obukhov length L.

3. Surface Boundary Layer Diffusivity

      Surface boundary layer diffusivity/viscosity profiles are calculated at model interfaces and smoothly matched to the interior diffusivities and viscosity. Boundary layer diffusivities and viscosity are parameterized as follows:

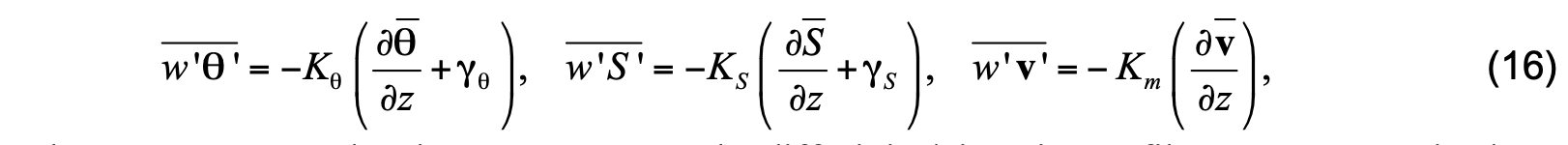
where γ_θ ,γ_S are nonlocal transport terms. The diffusivity/viscosity profiles are parameterized as

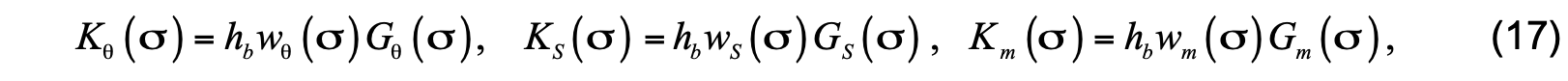
where G is a smooth shape function represented by a third-order polynomial function

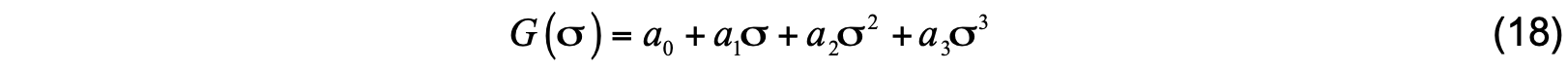
That is determined separately for each model variable. The salinity/scalar velocity scale w_S is estimated using (15). The potential temperature and momentum velocity scales w_θ, w_m are also estimated from equations analogous to (15), but with the two constants replaced by a_θ, c_θ and a_m, c_m, respectively. Since turbulent eddies do not cross ocean surface, all K coefficients are zero there, which requires that a₀ = 0.The remaining coefficients of the shape function for a given variable are chosen to satisfy requirements of Monin-Obukhov similarity theory, and also to insure that the resulting value and first vertical derivative of the boundary layer K -profile match the value and first derivative of the interior ν profile for the same variable calculated using (2) through (7) and (8) through (12).
      Application of this procedure is illustrated here for potential temperature only. The matching yields

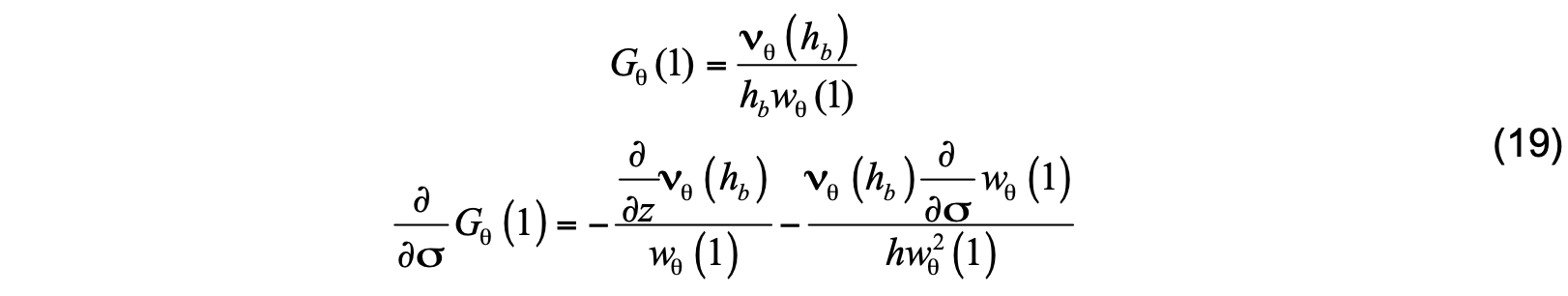
After determining the coefficients in (18), the K profile is calculated using

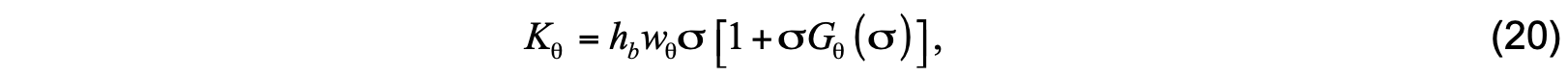
where

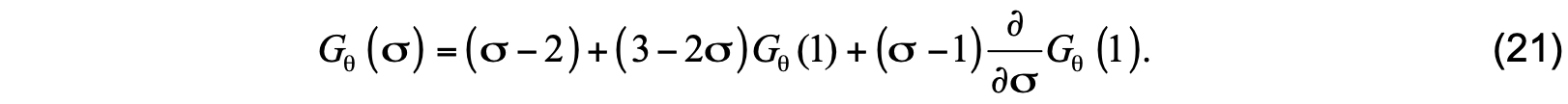
At model interfaces within the surface boundary layer, the K profile for potential temperature is provided by (20). At model interfaces below the boundary layer, the K profile equals the interior diffusivity ( K_θ = ν_θ ).
The nonlocal flux terms in (16) kick in when the surface forcing is destabilizing. The KPP model parameterizes nonlocal flux only for scalar variables. Although nonlocal fluxes may also be significant for momentum, the form that these fluxes take is presently not known. (Large et al., 1994). The nonlocal fluxes for scalar variables are parameterized as

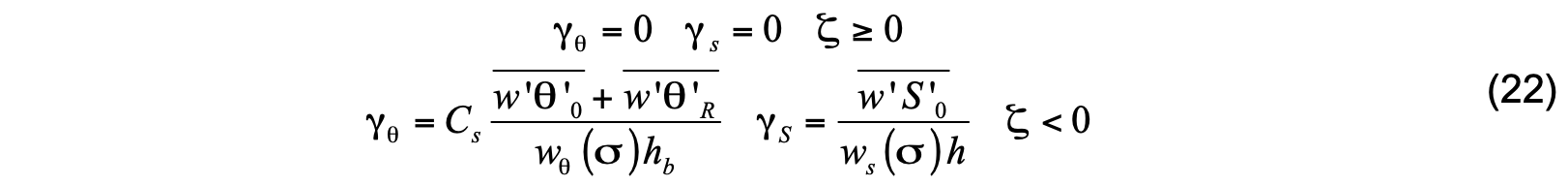
where ζ is a stability parameter equal to d / L and L is the Monin-Obukhov length. The terms and are surface fluxes while the term is the contribution of penetrating shortwave radiation.

4. Implementation

      Given the K profiles for T, S, and momentum at the pressure grid points, the one-dimensional vertical diffusion equation is solved at each grid point by formulating a matrix equation and inverting a tri-diagonal matrix (Appendix C). After solving the equation for all variables at the pressure grid points (including velocity components interpolated from the momentum grid points), the KPP procedure is repeated beginning with equation (1) using the new profiles of all variables. The user can choose how many of these iterations are performed. In practice, two iterations are generally found to be adequate. Mixed layer thickness is diagnosed at the pressure grid points based through vertical interpolation to the depth where density exceeds the surface layer density by a prescribed amount.
      After completing the mixing at pressure grid points, mixing is performed at the momentum grid points. Instead of repeating the entire KPP procedure, the Km profiles estima ted at the pressure grid points during the final iteration is horizontally interpolated to the u and v grid points, then the vertical diffusion equation is solved.

References

Large, W. G., J. C. McWilliams, and S. C. Doney, 1994: Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Rev. Geophys., 32, 363-403.

Peters, H., M. C. Gregg, and J. M. Toole, 1988: On the parameterization of equatorial turbulence. J. Geophys. Res., 93, 1199-1218.