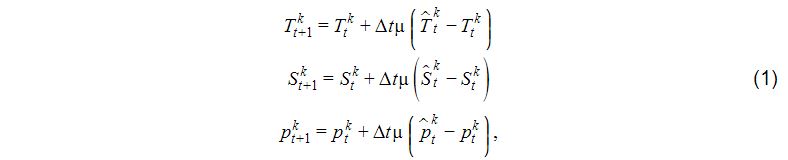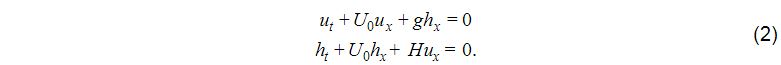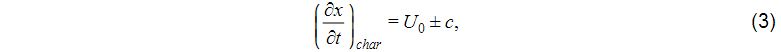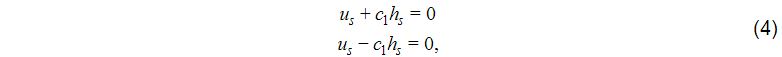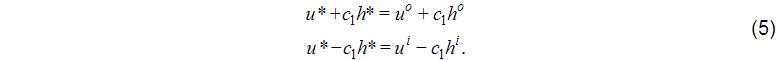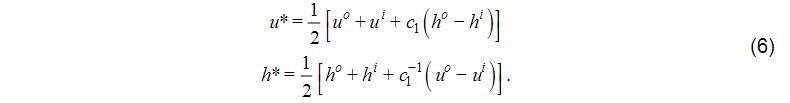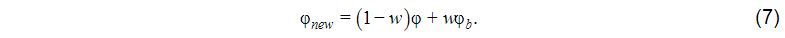Boundary conditions in HYCOM

Overview

HYCOM versions 1.0 and 2.0 are equipped with two types of boundary conditions: Newtonian relaxation in sponge layers, and full open-ocean boundary conditions. Both of these types are summarized in this document. The full open-ocean boundary conditions were not implemented as if the initial release of HYCOM 2.0, but since have been activated and tested.

Relaxation Boundary Conditions

HYCOM 1.0/2.0 contains a simple Newtonian relaxation scheme that can be used for sponge boundary zones, or more generally for relaxation to climatology within any model subdomain specified by the user. Within relaxation boundary zones, temperature, salinity, and vertical coordinate pressure levels are updated as follows for each time step:

$\begin{array}{c}{T_{t+1}^{k}=T_{t}^{k}+\Delta t \mu\left(\hat{T}{t}^{k}-T{t}^{k}\right)} \ {S_{t+1}^{k}=S_{t}^{k}+\Delta t \mu\left(\hat{S}{t}^{k}-S{t}^{k}\right)} \ {p_{t+1}^{k}=p_{t}^{k}+\Delta t \mu\left(\hat{p}{t}^{k}-p{t}^{k}\right)}\end{array}$

where the hat denotes Levitus climatology, k is the layer or interface number, and μ^-1 is the relaxation time scale. The user specifies the values of μ^-1 at each grid point, setting it to nonzero values where relaxation is to be performed. This results in a two-dimensional mask that defines the relaxation zones. Software is provided with HYCOM 1.0/2.0 that first horizontally interpolated Levitus climatology to model grid points at the original z levels, then transforms these vertical profiles to isopycnic coordinates at each model grid point. Thus, the profiles of μT, Ŝ, and μp used in (1) are isopycnic beneath the surface mixed layer.When HYCOM is run with isopycnic vertical coordinates (MICOM mode), temperature and salinity are both relaxed in the non-isopycnic mixed layer (layer 1) while salinity only is relaxed in deeper layers with temperature diagnosed from the equation of state to preserve the isopycnic reference density.

When HYCOM is run with isopycnic vertical coordinates (MICOM mode), temperature and salinity are both relaxed in the non-isopycnic mixed layer (layer 1) while salinity only is relaxed in deeper layers with temperature diagnosed from the equation of state to preserve the isopycnic reference density. When HYCOM is run with hybrid vertical coordinates, both temperature and salinity are relaxed in the upper n_hyb layers, where n_hyb is the user-specified number of hybrid layers, and salinity alone is relaxed in deeper layers with temperature diagnosed from the equation of state. When HYCOM is run with hybrid coordinates, all pressure interfaces are relaxed to climatology. When the model is run with isopycnic coordinates, all interfaces except 2 are relaxed to avoid adjusting the mixed layer base. Of course, all interfaces greater than 2 are prevented from becoming shallower than interface 2.

Open Boundary Conditions

Due to the fundamental ill posedness of the open boundary value problem in hydrostatic models (e.g. Oliger and Sundstrom, 1978), limited-area modeling with the primitive equations is more an art than a science. Open boundary conditions that have worked reasonably well in MICOM, and that have been adapted for HYCOM, are discussed here.

The main features of the open boundary scheme are as follows:

No distinction is made between inflow and outflow boundaries.
Boundary conditions for the barotropic and baroclinic mode are formulated separately.
The well-posed boundary conditions developed by Browning and Kreiss (1982, 1986), which work well in single-layer, shallow-water models, are applied to the barotropic mode, specifically the pressure field and normal velocity component.
Barotropic tangential velocity components are prescribed.
Baroclinic velocities normal to the boundary, as well as total (barotropic plus baroclinic) mass fluxes, are prescribed.
Baroclinic tangential velocity components are nudged toward prescribed values.
Other boundary conditions for the baroclinic mode are applied not only at points directly on the boundary, but in a finite-width “sponge” zone. They include interface pressure nudging, damping of the tendency term in the continuity equation, and enhanced viscosity in the momentum equations.

Details

The approach in item 1 above is taken in recognition of the fact that, regardless of the direction of the physical flow, information generally passes through the boundary in both directions. Making a distinction between inflow and outflow boundaries is therefore justified only with regard to advection of material properties, such as temperature, salinity, and potential vorticity.

Concerning item 3, Browning and Kreiss (1982, 1986) suggest that well-posed boundary conditions for modeling fluid flow in open domains can be derived from the theory of characteristics. In the case of two independent variables x,t, characteristics are curves x(t), which, if used as coordinate axes, reduce a set of coupled p.d.e.’s to a set of uncoupled o.d.e.’s.They arise during attempts to construct, through Taylor series expansion, the solution of a system of p.d.e.’s in the vicinity of a boundary curve in x,_t_i space along which the dependent variables and their normal derivatives are prescribed. Specifically, characteristics are curves that are unsuitable as boundary curves because the Taylor series coefficients cannot be uniquely determined from conditions prescribed along these curves.

Consider a simple hyperbolic system describing gravity wave propagation in a shallow fluid layer moving at speed U:

Equation 1

There are two sets of characteristics in this problem; their respective slopes in the x,t plane are

Equation 2

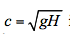
where c=RSgH is the gravity wave phase speed. Following the characteristics in x,t space is equivalent to tracking gravity waves that propagate upstream and downstream through the moving fluid.

The o.d.e.’s obtained by transforming x,t derivatives in the set of p.d.e.’s in (2) into derivatives taken along characteristics are

Equation 4

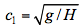
where Equation 3 and subscript s denotes differentiation along a characteristic. After integration over s, these equations state that u + c₁h and u - c₁h, respectively, are constant along the two sets of characteristics. The solution at a given point x,t can therefore be constructed by superimposing ,uh combinations carried along the two characteristics intersecting at x,t. This applies to interior as well as boundary points.

Let c>>U₀>0. On the upstream or “western” boundary, two characteristics, U₀-c going from west to east and 0Uc− going from east to west, bring in information from the exterior (provided by observations or a coarse-mesh model) and from the interior, respectively. The combination of these two characteristics yields the final boundary values of u and h. If superscript o denotes values obtained from the outer coarse-mesh model or data, i denotes values from the inner, fine-mesh model, and * denotes the actual boundary values, we have

Equation 5

This is a system of two equations for the two sought-after boundary values u*,h*. The solutions are

Equation 6

Boundary conditions for the case U₀<0 and the eastern boundary are analogous. If the model contains thermodynamic variables satisfying conservation laws dominated by advection processes, the method of characteristics suggests that these variables should be updated by coarse mesh fields or data at inflow points, and from within the model at outflow points.

Concerning item 5 above, prescribing the mass flux across boundaries is the most direct way to stabilize the time-mean circulation in subbasins forced by strong inflow/outflow. Concerning item 6 above, nudging is performed by replacing a grid point value φ by a linear combination of φ and a prescribed value φ_b.

Equation 7

If nudging is performed in a finite-width sponge zone, the weight w should gradually increase from zero in the interior of the domain to a finite value ≤1 at the boundary. The width of the sponge zone where w>0 and the rate at which w increases toward the boundary is best determined by experimentation.

The same goes for the viscosity enhancement factor and the damping factor applied to the layer thickness tendency. The damping factor should increase from near-zero at the domain boundary to a value of 1 at the inner edge of the sponge zone. Viscosity may be increased stepwise to as much as 5 or even 10 times its value outside the sponge zone.

References

Browning, G. L. and Kreiss, H.-O., 1982: Initialization of the shallow water equations with open boundaries by the bounded derivative method. Tellus, 34, 334-351.

Browning, G. L. and Kreiss, H.-O., 1986: Scaling and computation of smooth atmospheric motions. Tellus, 38A, 295-313.

Oliger, J. and A. Sundstrom, 1978: Theoretical and practical aspects of some initial boundary value problems in fluid mechanics. SIAM Appl. Math., 35, 419-446

Center for Ocean-Atmospheric Prediction Studies (COAPS)