What It Is and How It Works

The Problem of Charged Particles Dynamics Simulation

Ef is particle dynamics simulation software. It's task is to trace evolution of large number of charged particles, such as electrons and ions, under action of external electromagnetic fields, taking particle-particle interaction into account.

1 - cathode, 2 - focusing electrodes that generate static electric field E, 3 - beam region, 4 - guiding system, typically employing static magnetic field B, 5 - extraction region.

The key elements of the problem are following:

• Particles that experience action of electromagnetic fields. Typically we consider electrons and various ions. Each particle is represented by it's position, momentum, charge and mass.
• Particle sources. Particles do not appear out of nowhere. Typically they are emitted from cathode (see the figure above), extracted from plasma chamber, or produced in ionizing collisions. Each source yields different kinds of particles and has different internal properties (e.g. cathode material or cathode temperature) that influence various properties of generated particles.
• External static or quasistatic electromagnetic fields. Such fields are typically generated by electrostatic lenses or solenoids (see fields E and B on the figure above).
• Device geometry. The shape and the alignment of the cathode and focusing system is significant for the shape of the beam. Parts of the device are typically designed in 3d-modelling software. In general, various conducting or dielectric regions represented by complex 3d-objects might present in the simulation volume.
• External electromagnetic radiation. Laser or microwave radiation can be used to shape particles' dynamics.

After these components are specified, it is necessary to specify time interval to simulate. The program divides the time interval into discrete time steps and traces evolution of the system from one time step to another.

Intuitive Introduction to Particle-in-Cell Method

The basis of the created program is a so-called “particle-in-cell” method. Initially suggested in the 1950s for hydrodynamics simulations and popularized in the 1960s for plasma research, it is well described in the literature [Hockney, Grigorev]. The method aims to model dynamics of a large number of charged particles in external electromagnetic fields taking into account particle-particle interaction.

First, the equations of motion of individual particles are discretized, so that time evolution can be viewed as a sequence of time steps. At each time step, forces acting on particles consist of two components: the external fields and particle self-interaction. The external fields are considered preset. As for particle-particle interaction, in principle it can be taken into account directly using Coulomb's law. However, computational complexity of such approach grows as a square of a number of particles N, and for a large N it becomes unacceptable. Approximate methods are necessary to treat it.

The idea of “particle-in-cell” is to approximately compute electromagnetic fields generated by the particles instead of calculating binary Coulomb forces between each pair of them. Such collective fields are obtained by numerically solving Maxwell's equations, which requires to perform spatial discretization of the simulation volume, approximate contribution of each particle to charge density and current at each node, and solve for potentials on the mesh using finite difference or finite element method. After the combined action of the external and particle-generated fields on each particle is computed, integration of the dynamics equations is performed.

In the simplest case, magnetic field, generated by particles, can be neglected, and only electric field is taken into account. This is called electrostatic particle-in-cell. In such case, electrostatic potential is related to charge distribution in the volume by Poisson's equation:

Electric charge density at each node rho is calculated by summing contributions to charge density from each particle. Exact amount of particle's contribution to the given node is controlled by particle-mesh interpolation function ("shape" of the particle). In the simplest case particle contributes charge only to the nearest nodes, i.e. to the nodes of it's embedding cell. Particle's charge is distributed between these nodes proportionally to distance between each of the nodes and the particle: the closer the node, the bigger the contribution.

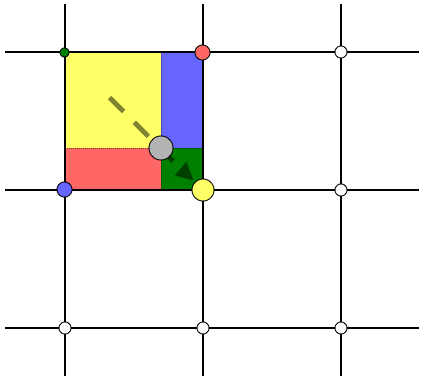
Image source: https://www.particleincell.com/2010/es-pic-method/
todo: redraw

After charge density at each node of the mesh is computed, potential values at the nodes can be calculated by solving Poisson's equation. Numerically evaluating a gradient of the potential, electric fields can be obtained.

todo: insert image

With values of electric field at each node known, it is necessary to interpolate these values back to particles' positions to obtain forces, acting on particles. Particle-mesh interpolation function is invoked here for the second time.

todo: insert image

Finally, when electric field acting on particle is obtained, it is possible to evaluate force on the particle and update it's position and momentum accordingly.

todo: insert image

Simulation Workflow

Basic workflow goes like this:

1. Create a config file describing your experiment.
2. Feed it to ef to perform simulation.
3. Process output files.

Config file is just a plain-text .ini file. In simple cases it can be created with any text editor. For more complex geometries, it can be generated with help of the FreeCAD plugin.

After config is prepared, starting the simulation is straightforward: issue a command like

    ./ef.out test.conf

In the standard output stream some information about simulation progress will be displayed.

After the simulation is finished, a number of *.h5 files will emerge in the output directory. Each file contains particles' position and momenta at different time step, as well as other supplemental information. .h5 is hdf5 format. Most languages and other tools used in scientific computing have a library to work with this format. Extracting relevant information from one or several files, it is possible to postprocess, plot, and analyze it.

Mathematical Model Description:

1. Time integration

For time integration, Boris scheme is used

where i is a number of time step and

\vec{v}_+ can be expressed in term of \vec{v}_- from the last two equations using algebraic manipulations or geometric considerations:

The Boris algorithm is notable for it's excellent long term accuracy.

2. Electrostatic PIC

On each time step, Poisson equation is solved

It is discretized using finite difference scheme (todo: add indices):

2.1) Particle-mesh

3. External fields

4. Fields from electrodes

Fields from electrodes are currently computed on the same mesh as PIC.