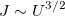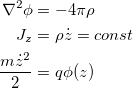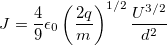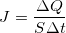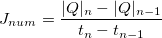Child Langmuir Law for Planar Diode

In this example, we are going to check the Child-Langmuir Law for a planar diode. It states, that for a steady flow of electrons between the plates serving as cathode and anode, a current density is related to a voltage on the plates as:

We'll check this relation by defining a planar diode configuration and measuring a current for several different voltage values.

Strictly speaking, Child-Langmuir in the form above is valid only for 1d case. A system of equations, describing a stable current is (Poisson's equation, continuity, energy conservation):

After solving the system, it is possible to obtain an equation for a potential between the plates, as well as a relation between the voltage and the current (todo: correct SI to CGS conversion )

To check this in simulation, we need to measure current for different voltages. Current density, by definition, is

Each inner region tracks total charge it absorbed. Therefore, to obtain current, we need to compute difference between total absorbed charge at two time steps and divide it by time step difference:

As of voltage, it is not possible to change voltage during the simulation. The only way is to run several simulations for several values of voltage. This will require preparation of several almost identical config files that only differ in voltage value and output file name.

A simple solution is to prepare template config and a script which will produce actual config files with different voltages.

The template config can be found here. It defines a planar diode modeled by two box-shaped inner regions and a source located near the anode.

...

[Inner_region_box.cathode]
potential = -0.0
box_x_left = 5.99
box_x_right = 0.01
box_y_bottom = 0.01
box_y_top = 5.99
box_z_near = 0.02
box_z_far = 0.1

[Particle_source_cylinder.cathode_emitter]
initial_number_of_particles = 3000
particles_to_generate_each_step = 3000
cylinder_axis_start_x = 3.0
cylinder_axis_start_y = 3.0
cylinder_axis_start_z = 0.11
cylinder_axis_end_x = 3.0
cylinder_axis_end_y = 3.0
cylinder_axis_end_z = 0.12
cylinder_radius = 0.03
mean_momentum_x = 0.0
mean_momentum_y = 0.0
mean_momentum_z = 9.5e-17
temperature = 0.0
charge = -1.5e-7
mass = 2.8e-25

[Inner_region_box.anode]
potential = +1.0
box_x_left = 5.99
box_x_right = 0.01
box_y_bottom = 0.01
box_y_top = 5.99
box_z_near = 0.9
box_z_far = 0.98

...

The amount of particles is relatively large to reduce statistical defects. We also have to take some precaution to prevent particles escape through side borders of the computation volume.

Boundary conditions are zero, magnetic field is off, particle interaction is enabled.

Time step has to be small to ensure the uniform flow of electrons, without any slices.

[pics illustrating sufficiently and insufficienly small time steps]

A script that generates actual configs from template is straightforward. It reads the whole template and replaces voltage line and output filename lines with necessary pregenerated values. Line numbers are hardcoded (which, of course, is not good).

After this script is executed, we'll get a number of config files. We have to run a simulation for each config:

for x in V*.conf
do
    ../../ef.out $x
done

This will result in a number of output files, corresponding to different voltages (warning: computation might take couple of hours of time and several Gb of HDD-space). For each voltage, we need to extract the current. We'll need a pair of out files, corresponding to two last time steps of simulation. This would allow to calculate current according to previously stated equation:

...

os.chdir("./")
# todo: remove hardcoding
prev_step_filename = "V*_*957.h5"
last_step_filename = "V*_*990.h5"
prev_step_vals = []
last_step_vals = []
for f in glob.glob( prev_step_filename ):
    prev_step_vals.append( get_time_potential_charge_absrbd_on_anode_from_h5( f ) )
for f in glob.glob( last_step_filename ):
    last_step_vals.append( get_time_potential_charge_absrbd_on_anode_from_h5( f ) )

prev_step_vals.sort( key = operator.itemgetter(1) )
last_step_vals.sort( key = operator.itemgetter(1) )

current = []
voltage = []
for (t1,V1,q1), (t2,V2,q2) in zip( prev_step_vals, last_step_vals ):
    print( t2 - t1, V2 - V1, q2 - q1 )
    current.append( abs( ( q2 - q1 ) ) / ( t2 - t1 ) )
    voltage.append( V1 )

...

Other part of the script is rather technical: it finds necessary out files and reads various parts of it.

Finally, volt-ampere characteristic can be plotted to check the Child-Langmuir law:

In 3d case we get different dependence that predicted by eqn 1, valid only for 1d. Linearisation of equation

[eqn]
J = a * U^(b) 
ln(J) = ln(a) + b ln(U)

allows to run least squares fit and obtain the value of coefficients a and b:

[code]

Agreement with theoretical value is reasonable.

The general view of what is going on:

Note how the beam radius decreases as voltage between plates is icreased (310V, 510V, 1010V):