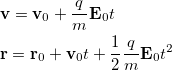Single Particle In Uniform Electric Field

todo: update and rewrite; use uniform electric field instead of boundary conditions

In this example, exact analytical trajectory of a charged particle moving in a uniform electric field is compared with results of numerical simulation.

In uniform electric field charged particle moves with uniform acceleration, directed along the field.

Part of a config file, regarding single particle, is similar to 'singe particle in free space'. As of uniform electric field, currently ef can not use any analytical expressions for fields, nor load precomputed numerical fields. However, a good approximation for uniform field is field between two parallel charged plates. The simplest way to model this in ef is to specify appropriate boundary conditions. We need nonzero potential difference on two opposing sides of the computational volume.

[Boundary conditions]
boundary_phi_left = 0.0
boundary_phi_right = 0.0
boundary_phi_bottom = 0.0
boundary_phi_top = 0.0
boundary_phi_near = 3.0
boundary_phi_far = -3.0

To ensure a good degree of field uniformity, we need distance between two "plates" (i.e. sides of the computational volume with potential difference) to be much less than size of the plates

[Spatial mesh]
grid_x_size = 10.0
grid_x_step = 0.25
grid_y_size = 10.0
grid_y_step = 0.25
grid_z_size = 1.0
grid_z_step = 0.01

Initial position of the particle had to be adjusted:

[Particle_source_box.emit_single_particle]
...
box_x_left = 5.00
box_x_right = 5.01
box_y_bottom = 5.00
box_y_top = 5.01
box_z_near = 0.10
box_z_far = 0.11
...

After the simulation, it is useful to glance over potential distribution in the volume. 3d figure is not very informative. Use 2d colormaps at XY and XZ planes at nodes near particle initial position. Relevant plotting script is [link].

The results are

Electric field is directed perpendicular to equipotential surfaces. It can be seen, that it the middle of computational region electric field is directed along Z.

Trajectories are plotted similarly to previous examples. Magnitude of electric field equals potential difference divided by distance between plates: [E_0 = - delta phi / d ][eqn]

Figures of trajectories: (todo: something wrong with kin. energy.)

Degree of field uniformity can be estimated by evaluating difference of field components near initial and final points of particle trajectory: [code]

For present choice of parameters:

( Exf - Exi ) / Ez0 = , 
( Eyf - Eyi ) / Ez0 = , 
( Ezf - Ezi ) / Ez0 = 

It should not be very significant.