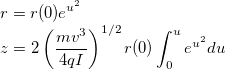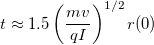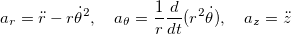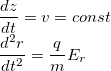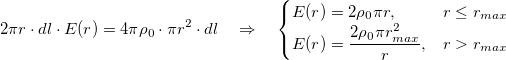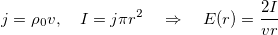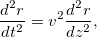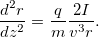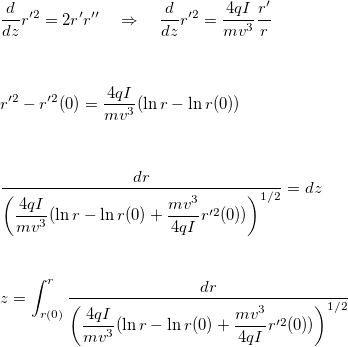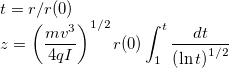Axially Symmetric Beam Contour

In this example (Google Colab version), an equation for a contour of an axially symmetric beam propagating in free space is checked.

# To run the example:
cd your-ef-dir; cd examples/axially_symmetric_beam_contour; sh run_example.sh

Suppose there is an axially symmetric charged particles beam propagating in free space. Under certain set of approximations, trajectory of a particle on the edge of the beam can be described by the following expressions:

where u is a parameter, v is speed of particles along the z axis, r(0) is initial radius and I is full current of the beam. Derivation of these relations can be found below.

These equations define a contour of the beam r(z). It is possible to perform a numerical simulation of a beam propagating in free space and plot particles coordinates on the X-Z or Y-Z plane. This will allow to compare the numerical profile with the analytical expression.

The beam will become e = 2.71 times wider than the initial at u = 1. For this value of the parameter, the integral in the z equation approximately equals to 1.46. Since the speed in the z-direction is assumed constant, it is possible to estimate the time needed for
particles to pass this distance as

Let's substitute some numerical values (see estimates.py). Suppose there is an electron beam (q = 4.8e-10 [cgs], m = 9.1e-28 [g]) with full current I = 0.1 [A] = 2.998e+08 [cgs] and initial radius r(0) = 0.5 [cm]. Energy of it's particles equals to 1 keV, so that speed is v = 1.808e+09 [cm/s]. For this beam to get 2.71 times wider (from 0.5 [cm] to 1.36 [cm]), it takes t = 2.632e-09 [s] seconds. This happens over a distance z = 4.632 [cm].

Let's use these estimates as a basis for config file parameters. Full simulation time is set to 3.0e-9 [s]. There is 100 time steps, with each 10th step written to file.

[Time grid]
total_time = 3.0e-9
time_save_step = 3.0e-10
time_step_size = 3.0e-11

The simulation domain is defined as

[Spatial mesh]
grid_x_size = 5.0
grid_x_step = 0.1
grid_y_size = 5.0
grid_y_step = 0.1
grid_z_size = 10.0
grid_z_step = 0.1

with z size approximately two times the estimated value, with 100 nodes in that direction. X and y sizes are 10 times the radius with 50 nodes in each direction.

The source is centered along the x and y axes and is close to origin along the z. For a time step dt = 3.00e-11 [s], to provide a current I = 0.1 [A] the source has to generate n = I * dt / q = 1.87e+07 particles each time step. This is not computationally feasible, so instead let's fix an amount of generated particles to 5000 at each step. The charge of macroparticles should be Q = I * dt / n = 1.799e-06 [cgs] To preserve charge-to-mass ratio, mass of the macroparticles should be set to M = Q / q_e * m_e = 3.672e-24 [g]. To have the same initial velocity as electrons, mean momentum should be set to p = M * v = 6.641e-15 [g * cm / s].

[Particle_source_cylinder.cathode_emitter]
initial_number_of_particles = 5000
particles_to_generate_each_step = 5000
cylinder_axis_start_x = 2.5
cylinder_axis_start_y = 2.5
cylinder_axis_start_z = 0.51
cylinder_axis_end_x = 2.5
cylinder_axis_end_y = 2.5
cylinder_axis_end_z = 0.52
cylinder_radius = 0.5
mean_momentum_x = 0
mean_momentum_y = 0
mean_momentum_z = 6.641e-15
temperature = 0.0
charge = -1.799e-6
mass = 3.672e-24

Potential is zero on each boundary of the domain.

[Boundary conditions]
boundary_phi_left = 0.0
boundary_phi_right = 0.0
boundary_phi_bottom = 0.0
boundary_phi_top = 0.0
boundary_phi_near = 0.0
boundary_phi_far = 0.0

After the simulation, X-Z coordinates of the particles are plotted. Numerical results

.....
r_num = h5file["/Particle_sources/cathode_emitter/position_x"]
z_num = h5file["/Particle_sources/cathode_emitter/position_z"]
.....
plt.plot( z_num, r_num, '.', label = "num" )

are compared with the analytical predictions

def beam_radius( u, r_0 ):
    return r_0 * np.exp( u ** 2 )

def beam_z( u, m, v, q, I, r_0 ):
    coeff = np.sqrt( m * v**3 / q / I ) * r_0
    subint = lambda t: np.exp( t * t )
    low_lim = 0
    up_lim = u
    integral_value = scipy.integrate.quad( subint, low_lim, up_lim )[0]  # (*1)
    return coeff * integral_value

.....

u_min = 0; u_max = 2; num_u_points = 100  # for u = 1, r = r(0) * 2.71812
u = np.linspace( u_min, u_max, num_u_points )
r_an = [ beam_radius( x, r_0 ) for x in u ]
r_an_upper = r_an + beam_axis_x_pos
r_an_lower = beam_axis_x_pos - r_an 
z_an = [ beam_z( x, m = m, v = v, q = q, I = I, r_0 = r_0 ) for x in u ]
z_an = z_an + emitter_z_pos
.....
plt.plot( z_an, r_an_upper, label = "theory", color = "g" )
plt.plot( z_an, r_an_lower, color = "g" )

(*1): Instead of integration, scipy.special.erf or scipy.special.erfi functions can be used.

The results of the simulation are following:

It can be seen, that divergence between the analytical contour and numerical simulation is more significant near the front of the beam (right side of the figure), than in it's body (the left side). This can be attributed to the fact, that the analytical expression was derived in assumption of zero electric field along the z axis E_z = 0. This assumption does not hold for particles on the front of the beam, which experience accelerating field from the particles behind them. Therefore, they move faster than the body of the beam and can travel longer distance before radial electric field widens their profile significantly.

[todo: check correctness] Another possible source of discrepancy lies in the assumption of constant charge density rho_0 made in the derivation of the analytical model. In practice, charge density is maximal near the center and decreases towards the edges. Therefore, the radial electric field experienced by the particles near the edges is not as strong as predicted by this assumption overestimating broadening of the beam.

Trajectory equations

In cylindrical coordinates components of the acceleration vector are given by

For a beam of charged particles in free space \dot{\theta} = 0 due to cylindrical symmetry. Besides, in paraxial approximation, E_z = 0 and v_z \equiv v = const. Therefore, equations of motion can be written as

Radial electric field can be found from Gauss theorem:

where charge density rho_0(r) is approximated by a constant rho_0.

Rewriting this expression in terms of electric current:

Passing from time derivative to derivative over z

it is possible to derive a trajectory equation from the equations of motion

Employing some arithmetical tricks, it is possible to integrate it:

For r'(0) = 0:

Substituting t = e^{u^2}:

References:

[Alyamovsky], paragraph 2.2; for trajectory equation: p. 40, eq. 2.34.