README.md

Lambda the Ultimate Pattern Factory

My first programming languages were Lisp, Scheme, and ML. When I later started to work in OO languages like C++ and Java I noticed that idioms that are standard vocabulary in functional programming (fp) were not so easy to achieve and required sophisticated structures. Books like Design Patterns: Elements of Reusable Object-Oriented Software were a great starting point to reason about those structures. One of my earliest findings was that several of the GoF-Patterns had a stark resemblance of structures that are built into in functional languages: for instance the strategy pattern corresponds to higher order functions in fp (more details see below).

Recently, while re-reading through the Typeclassopedia I thought it would be a good exercise to map the structure of software design-patterns to the concepts found in the Haskell type class library and in functional programming in general.

By searching the web I found some blog entries studying specific patterns, but I did not come across any comprehensive study. As it seemed that nobody did this kind of work yet I found it worthy to spend some time on it and write down all my findings on the subject.

I think this kind of exposition could be helpful if you are:

• a programmer with an OO background who wants to get a better grip on how to implement more complex designs in functional programming
• a functional programmer who wants to get a deeper intuition for type classes.
• studying the Typeclassopedia and are looking for an accompanying reading providing example use cases and working code.

This project is work in progress, so please feel free to contact me with any corrections, adjustments, comments, suggestions and additional ideas you might have. Please use the Issue Tracker to enter your requests.

Table of contents

• Lambda the ultimate pattern factory
• The Patternopedia
  • Data Transfer Object → Functor
  • Singleton → Applicative
  • Pipeline → Monad
  • NullObject → Maybe Monad
  • Interpreter → Reader Monad
  • Aspect Weaving → Monad Transformers
  • Composite → SemiGroup → Monoid
  • Visitor → Foldable
  • Iterator → Traversable
  • The Pattern behind the Patterns → Category
  • Fluent Api → Comonad
• Beyond type class patterns
  • Dependency Injection → Parameter Binding, Partial Application
  • Command → Functions as First Class Citizens
  • Adapter → Function Composition
  • Template Method → type class default functions
  • Creational Patterns
    • Abstract Factory → functions as data type values
    • Builder → record syntax, smart constructor
• Functional Programming Patterns
  • Higher Order Functions
  • Map Reduce
  • Lazy Evaluation
  • Reflection
• Conclusions
• Some related links

The Patternopedia

The Typeclassopedia is a now classic paper that introduces the Haskell type classes by clarifying their algebraic and category-theoretic background. In particular it explains the relationships among those type classes.

In this chapter I'm taking a tour through the Typeclassopedia from a design pattern perspective. For each of the Typeclassopedia type classes I try to explain how it corresponds to structures applied in software design patterns.

As a reference map I have included the following chart that depicts the Relationships between type classes covered in the Typeclassopedia:

• Solid arrows point from the general to the specific; that is, if there is an arrow from Foo to Bar it means that every Bar is (or should be, or can be made into) a Foo.
• Dotted lines indicate some other sort of relationship.
• Monad and ArrowApply are equivalent.
• Apply and Comonad are greyed out since they are not actually (yet?) in the standard Haskell libraries ∗.

Data Transfer Object → Functor

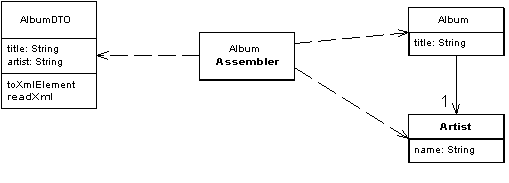
In the field of programming a data transfer object (DTO) is an object that carries data between processes. The motivation for its use is that communication between processes is usually done resorting to remote interfaces (e.g., web services), where each call is an expensive operation. Because the majority of the cost of each call is related to the round-trip time between the client and the server, one way of reducing the number of calls is to use an object (the DTO) that aggregates the data that would have been transferred by the several calls, but that is served by one call only. (quoted from Wikipedia

Data Transfer Object is a pattern from Martin Fowler's Patterns of Enterprise Application Architecture. It is typically used in multi-layered applications where data is transferred between backends and frontends.

The aggregation of data usually also involves a denormalization of data structures. As an example, please refer to the following diagram where two entities from the backend (Album and Artist) are assembled to a compound denormalized DTO AlbumDTO:

Of course, there is also an inverse mapping from AlbumDTO to Album which is not shown in this diagram.

In Haskell Album, Artist and AlbumDTO can be represented as data types with record notation:

data Album = Album {
    title       :: String
  , publishDate :: Int
  , labelName   :: String
  , artist      :: Artist
} deriving (Show)

data Artist = Artist {
    publicName :: String
  , realName   :: Maybe String
} deriving (Show)

data AlbumDTO = AlbumDTO {
    albumTitle  :: String
  , published   :: Int
  , label       :: String
  , artistName  :: String
} deriving (Show, Read)

The transfer from an Album to an AlbumDTO and vice versa can be achieved by two simple functions, that perfom the intended field wise mappings:

toAlbumDTO :: Album -> AlbumDTO
toAlbumDTO Album {title = t, publishDate = d, labelName = l, artist = a} =
  AlbumDTO {albumTitle = t, published = d, label = l, artistName = (publicName a)}

toAlbum :: AlbumDTO -> Album
toAlbum AlbumDTO {albumTitle = t, published = d, label = l, artistName = n} =
  Album {title = t, publishDate = d, labelName = l, artist = Artist {publicName = n, realName = Nothing}}

In this few lines we have covered the basic idea of the DTO pattern.

Now, let's consider the typical situation that you don't have to transfer only a single Album instance but a whole list of Album instances, e.g.:

albums :: [Album]
albums =
    [
      Album {title = "Microgravity",
             publishDate = 1991,
             labelName = "Origo Sound",
             artist = Artist {publicName = "Biosphere", realName = Just "Geir Jenssen"}}
    , Album {title = "Apollo - Atmospheres & Soundtracks",
             publishDate = 1983,
             labelName = "Editions EG",
             artist = Artist {publicName = "Brian Eno", realName = Just "Brian Peter George St. John le Baptiste de la Salle Eno"}}
    ]

In this case we have to apply the toAlbumDTO function to all elements of the list. In Haskell this higher order operation is called map:

map :: (a -> b) -> [a] -> [b]
map _f []    = []
map f (x:xs) = f x : map f xs

map takes a function f :: (a -> b) (a function from type a to type b) and an [a] list and returns a [b] list. The b elements are produced by applying the function f to each element of the input list. Applying toAlbumDTO to a list of albums can thus be done in the Haskell REPL GHCi as follows:

λ> map toAlbumDTO albums
[AlbumDTO {albumTitle = "Microgravity", published = 1991, label = "Origo Sound", artistName = "Biosphere"},
 AlbumDTO {albumTitle = "Apollo - Atmospheres & Soundtracks", published = 1983, label = "Editions EG", artistName = "Brian Eno"}]

This mapping of functions over lists is a basic technique known in many functional languages. In Haskell further generalises this technique with the concept of the Functor type class.

The Functor class is the most basic and ubiquitous type class in the Haskell libraries. A simple intuition is that a Functor represents a “container” of some sort, along with the ability to apply a function uniformly to every element in the container. For example, a list is a container of elements, and we can apply a function to every element of a list, using map. As another example, a binary tree is also a container of elements, and it’s not hard to come up with a way to recursively apply a function to every element in a tree.

Another intuition is that a Functor represents some sort of “computational context”. This intuition is generally more useful, but is more difficult to explain, precisely because it is so general.

Quoted from Typeclassopedia

Basically, all instances of the Functor type class must provide a function fmap:

class  Functor f  where
    fmap :: (a -> b) -> f a -> f b

For Lists the implementation is simply the map function that we already have seen above:

instance Functor [] where
    fmap = map

Functors have interesting properties, they fulfill the two so called functor laws, which are part of the definition of a mathematical functor:

fmap id = id                        -- (1)
fmap (g . h) = (fmap g) . (fmap h)  -- (2)

The first law (1) states that mapping the identity function over every item in a container has no effect.

The second (2) says that mapping a composition of two functions over every item in a container is the same as first mapping one function, and then mapping the other.

These laws are very useful when we consider composing complex mappings from simpler operations.

Say we want to extend our DTO mapping functionality by also providing some kind of marshalling. For a single album instance, we can use function composition (f . g) x == f (g x), which is defined in Haskell as:

(.) :: (b -> c) -> (a -> b) -> a -> c
(.) f g x = f (g x)

In the following GHCi session we are using (.) to first convert an Album to its AlbumDTO representation and then turn that into a String by using the show function:

λ> album1 = albums !! 0
λ> print album1
Album {title = "Microgravity", publishDate = 1991, labelName = "Origo Sound", artist = Artist {publicName = "Biosphere", realName = Just "Geir Jenssen"}}
λ> marshalled = (show . toAlbumDTO) album1
λ> :t marshalled
marshalled :: String
λ> print marshalled
"AlbumDTO {albumTitle = \"Microgravity\", published = 1991, label = \"Origo Sound\", artistName = \"Biosphere\"}"

As we can rely on the functor law fmap (g . h) = (fmap g) . (fmap h) we can use fmap to use the same composed function on any functor, for example our list of albums:

λ> fmap (show . toAlbumDTO) albums
["AlbumDTO {albumTitle = \"Microgravity\", published = 1991, label = \"Origo Sound\", artistName = \"Biosphere\"}",
 "AlbumDTO {albumTitle = \"Apollo - Atmospheres & Soundtracks\", published = 1983, label = \"Editions EG\", artistName = \"Brian Eno\"}"]

We can build more complex mappings by chaining multiple functions, to produce for example a gzipped byte string output:

λ> gzipped = (compress . pack . show . toAlbumDTO) album1

As the sequence of operation must be read from right to left for the (.) operator this becomes quite unintuitive for longer sequences. Thus, Haskellers often use the flipped version of (.), (>>>) which is defined as:

f >>> g = g . f

Using (>>>) the intent of our composition chain becomes much clearer (at least when you are trained to read from left to right):

λ> gzipped = (toAlbumDTO >>> show >>> pack >>> compress) album1

Unmarshalling can be defined using the inverse operations:

λ> unzipped = (decompress >>> unpack >>> read >>> toAlbum) gzipped
λ> :t unzipped
unzipped :: Album
λ> print unzipped
Album {title = "Microgravity", publishDate = 1991, labelName = "Origo Sound", artist = Artist {publicName = "Biosphere", realName = Nothing}}

Of course, we can use fmap to apply such composed mapping function to any container type instantiating the Functor type class:

λ> marshalled   = fmap (toAlbumDTO >>> show >>> pack >>> compress) albums
λ> unmarshalled = fmap (decompress >>> unpack >>> read >>> toAlbum) marshalled
λ> print unmarshalled
[Album {title = "Microgravity", publishDate = 1991, labelName = "Origo Sound", artist = Artist {publicName = "Biosphere", realName = Nothing}},
 Album {title = "Apollo - Atmospheres & Soundtracks", publishDate = 1983, labelName = "Editions EG", artist = Artist {publicName = "Brian Eno", realName = Nothing}}]

Sourcecode for this section

Singleton → Applicative

"The singleton pattern is a software design pattern that restricts the instantiation of a class to one object. This is useful when exactly one object is needed to coordinate actions across the system." (quoted from Wikipedia

The singleton pattern ensures that multiple requests to a given object always return one and the same singleton instance. In functional programming this semantics can be achieved by let:

let singleton = someExpensiveComputation
in  mainComputation

--or in lambda notation:
(\singleton -> mainComputation) someExpensiveComputation

Via the let-Binding we can thread the singleton through arbitrary code in the in block. All occurences of singleton in the mainComputationwill point to the same instance.

Type classes provide several tools to make this kind of threading more convenient or even to avoid explicit threading of instances.

Using Applicative Functor for threading of singletons

The following code defines a simple expression evaluator:

data Exp e = Var String
           | Val e
           | Add (Exp e) (Exp e)
           | Mul (Exp e) (Exp e)

-- the environment is a list of tuples mapping variable names to values of type e
type Env e = [(String, e)]

-- a simple evaluator reducing expression to numbers
eval :: Num e => Exp e -> Env e -> e
eval (Var x)   env = fetch x env
eval (Val i)   env = i
eval (Add p q) env = eval p env + eval q env  
eval (Mul p q) env = eval p env * eval q env

eval is a classic evaluator function that recursively evaluates sub-expression before applying + or *. Note how the explicit envparameter is threaded through the recursive eval calls. This is needed to have the environment avalailable for variable lookup at any recursive call depth.

If we now bind env to a value as in the following snippet it is used as an immutable singleton within the recursive evaluation of eval exp env.

main = do
  let exp = Mul (Add (Val 3) (Val 1))
                (Mul (Val 2) (Var "pi"))
      env = [("pi", pi)]
  print $ eval exp env

Experienced Haskellers will notice the "eta-reduction smell" in eval (Var x) env = fetch x env which hints at the possibilty to remove env as an explicit parameter. We can not do this right away as the other equations for eval do not allow eta-reduction. In order to do so we have to apply the combinators of the Applicative Functor:

class Functor f => Applicative f where
    pure  :: a -> f a
    (<*>) :: f (a -> b) -> f a -> f b

instance Applicative ((->) a) where
    pure        = const
    (<*>) f g x = f x (g x)

This Applicative allows us to rewrite eval as follows:

eval :: Num e => Exp e -> Env e -> e
eval (Var x)   = fetch x
eval (Val i)   = pure i
eval (Add p q) = pure (+) <*> eval p  <*> eval q  
eval (Mul p q) = pure (*) <*> eval p  <*> eval q

Any explicit handling of the variable env is now removed. (I took this example from the classic paper Applicative programming with effects which details how pure and <*> correspond to the combinatory logic combinators K and S.)

Sourcecode for this section

Pipeline → Monad

In software engineering, a pipeline consists of a chain of processing elements (processes, threads, coroutines, functions, etc.), arranged so that the output of each element is the input of the next; the name is by analogy to a physical pipeline. (Quoted from: Wikipedia

The concept of pipes and filters in Unix shell scripts is a typical example of the pipeline architecture pattern.

$ echo "hello world" | wc -w | xargs printf "%d*3\n" | bc -l
6

This works exactly as stated in the wikipedia definition of the pattern: the output of echo "hello world" is used as input for the next command wc -w. The ouptput of this command is then piped as input into xargs printf "%d*3\n" and so on. On the first glance this might look like ordinary function composition. We could for instance come up with the following approximation in Haskell:

((3 *) . length . words) "hello world"
6

But with this design we missed an important feature of the chain of shell commands: The commands do not work on elementary types like Strings or numbers but on input and output streams that are used to propagate the actual elementary data around. So we can't just send a String into the wc command as in "hello world" | wc -w. Instead we have to use echo to place the string into a stream that we can then use as input to the wc command:

> echo "hello world" | wc -w

So we might say that echo injects the String "hello world" into the stream context. We can capture this behaviour in a functional program like this:

-- The Stream type is a wrapper around an arbitrary payload type 'a'
newtype Stream a = Stream a deriving (Show)

-- echo injects an item of type 'a' into the Stream context
echo :: a -> Stream a
echo = Stream

-- the 'andThen' operator used for chaining commands
infixl 7 |>
(|>) :: Stream a -> (a -> Stream b) -> Stream b
Stream x |> f = f x


-- echo and |> are used to create the actual pipeline
pipeline :: String -> Stream Int
pipeline str =
  echo str |> echo . length . words |> echo . (3 *)
-- now executing the program in ghci repl:
ghci> pipeline "hello world"
Stream 6  

The echo function injects any input into the Stream context:

ghci> echo "hello world"
Stream "hello world"

The |> (pronounced as "andThen") does the function chaining:

ghci> echo "hello world" |> echo . words
Stream ["hello","world"]

The result of |> is of type Stream b that's why we cannot just write echo "hello world" |> words. We have to use echo to create a Stream output that can be digested by a subsequent |>.

The interplay of a Context type Stream a and the functions echo and |> is a well known pattern from functional languages: it's the legendary Monad. As the Wikipedia article on the pipeline pattern states:

Pipes and filters can be viewed as a form of functional programming, using byte streams as data objects; more specifically, they can be seen as a particular form of monad for I/O.

There is an interesting paper available elaborating on the monadic nature of Unix pipes: Monadic Shell.

Here is the definition of the Monad type class in Haskell:

class Applicative m => Monad m where
    -- | Sequentially compose two actions, passing any value produced
    -- by the first as an argument to the second.
    (>>=)  :: m a -> (a -> m b) -> m b

    -- | Inject a value into the monadic type.
    return :: a -> m a
    return = pure

By looking at the types of >>= and return it's easy to see the direct correspondence to |> and echo in the pipeline example above:

    (|>)   :: Stream a -> (a -> Stream b) -> Stream b
    echo   :: a -> Stream a

Mhh, this is nice, but still looks a lot like ordinary composition of functions, just with the addition of a wrapper. In this simplified example that's true, because we have designed the |> operator to simply unwrap a value from the Stream and bind it to the formal parameter of the subsequent function:

Stream x |> f = f x

But we are free to implement the andThen operator in any way that we seem fit as long we maintain the type signature and the monad laws. So we could for instance change the semantics of >>= to keep a log along the execution pipeline:

-- The DeriveFunctor Language Pragma provides automatic derivation of Functor instances
{-# LANGUAGE DeriveFunctor #-}

-- a Log is just a list of Strings
type Log = [String]

-- the Stream type is extended by a Log that keeps track of any logged messages
newtype LoggerStream a = LoggerStream (a, Log) deriving (Show, Functor)

instance Applicative LoggerStream where
  pure = return
  LoggerStream (f, _) <*> r = fmap f r  

-- our definition of the Logging Stream Monad:
instance Monad LoggerStream where
  -- returns a Stream wrapping a tuple of the actual payload and an empty Log
  return a = LoggerStream (a, [])

  -- we define (>>=) to return a tuple (composed functions, concatenated logs)
  m1 >>= m2  = let LoggerStream(f1, l1) = m1
                   LoggerStream(f2, l2) = m2 f1
               in LoggerStream(f2, l1 ++ l2)

-- compute length of a String and provide a log message
logLength :: String -> LoggerStream Int
logLength str = let l = length(words str)
                in LoggerStream (l, ["length(" ++ str ++ ") = " ++ show l])

-- multiply x with 3 and provide a log message
logMultiply :: Int -> LoggerStream Int
logMultiply x = let z = x * 3
                in LoggerStream (z, ["multiply(" ++ show x ++ ", 3" ++") = " ++ show z])

-- the logging version of the pipeline
logPipeline :: String -> LoggerStream Int
logPipeline str =
  return str >>= logLength >>= logMultiply

-- and then in Ghci:
> logPipeline "hello logging world"
LoggerStream (9,["length(hello logging world) = 3","multiply(3, 3) = 9"])

What's noteworthy here is that Monads allow to make the mechanism of chaining functions explicit. We can define what andThen should mean in our pipeline by choosing a different Monad implementation. So in a sense Monads could be called programmable semicolons

To make this statement a bit clearer we will have a closer look at the internal workings of the Maybe Monad in the next section.

Sourcecode for this section

NullObject → Maybe Monad

[...] a null object is an object with no referenced value or with defined neutral ("null") behavior. The null object design pattern describes the uses of such objects and their behavior (or lack thereof). Quoted from Wikipedia

In functional programming the null object pattern is typically formalized with option types:

[...] an option type or maybe type is a polymorphic type that represents encapsulation of an optional value; e.g., it is used as the return type of functions which may or may not return a meaningful value when they are applied. It consists of a constructor which either is empty (named None or Nothing), or which encapsulates the original data type A (written Just A or Some A). Quoted from Wikipedia

(See also: Null Object as Identity)

In Haskell the most simple option type is Maybe. Let's directly dive into an example. We define a reverse index, mapping songs to album titles. If we now lookup up a song title we may either be lucky and find the respective album or not so lucky when there is no album matching our song:

import           Data.Map (Map, fromList)
import qualified Data.Map as Map (lookup) -- avoid clash with Prelude.lookup

-- type aliases for Songs and Albums
type Song   = String
type Album  = String

-- the simplified reverse song index
songMap :: Map Song Album
songMap = fromList
    [("Baby Satellite","Microgravity")
    ,("An Ending", "Apollo: Atmospheres and Soundtracks")]

We can lookup this map by using the function Map.lookup :: Ord k => k -> Map k a -> Maybe a.

If no match is found it will return Nothing if a match is found it will return Just match:

ghci> Map.lookup "Baby Satellite" songMap
Just "Microgravity"
ghci> Map.lookup "The Fairy Tale" songMap
Nothing

Actually the Maybe type is defined as:

data  Maybe a  =  Nothing | Just a
    deriving (Eq, Ord)

All code using the Map.lookup function will never be confronted with any kind of Exceptions, null pointers or other nasty things. Even in case of errors a lookup will always return a properly typed Maybe instance. By pattern matching for Nothing or Just a client code can react on failing matches or positive results:

    case Map.lookup "Ancient Campfire" songMap of
        Nothing -> print "sorry, could not find your song"
        Just a  -> print a

Let's try to apply this to an extension of our simple song lookup. Let's assume that our music database has much more information available. Apart from a reverse index from songs to albums, there might also be an index mapping album titles to artists. And we might also have an index mapping artist names to their websites:

type Song   = String
type Album  = String
type Artist = String
type URL    = String

songMap :: Map Song Album
songMap = fromList
    [("Baby Satellite","Microgravity")
    ,("An Ending", "Apollo: Atmospheres and Soundtracks")]

albumMap :: Map Album Artist
albumMap = fromList
    [("Microgravity","Biosphere")
    ,("Apollo: Atmospheres and Soundtracks", "Brian Eno")]

artistMap :: Map Artist URL
artistMap = fromList
    [("Biosphere","http://www.biosphere.no//")
    ,("Brian Eno", "http://www.brian-eno.net")]

lookup' :: Ord a => Map a b -> a -> Maybe b
lookup' = flip Map.lookup

findAlbum :: Song -> Maybe Album
findAlbum = lookup' songMap

findArtist :: Album -> Maybe Artist
findArtist = lookup' albumMap

findWebSite :: Artist -> Maybe URL
findWebSite = lookup' artistMap

With all this information at hand we want to write a function that has an input parameter of type Song and returns a Maybe URL by going from song to album to artist to website url:

findUrlFromSong :: Song -> Maybe URL
findUrlFromSong song =
    case findAlbum song of
        Nothing    -> Nothing
        Just album ->
            case findArtist album of
                Nothing     -> Nothing
                Just artist ->
                    case findWebSite artist of
                        Nothing  -> Nothing
                        Just url -> Just url

This code makes use of the pattern matching logic described before. It's worth to note that there is some nice circuit breaking happening in case of a Nothing. In this case Nothing is directly returned as result of the function and the rest of the case-ladder is not executed. What's not so nice is "the dreaded ladder of code marching off the right of the screen" (quoted from Real World Haskell).

For each find function we have to repeat the same ceremony of pattern matching on the result and either return Nothing or proceed with the next nested level.

The good news is that it is possible to avoid this ladder. We can rewrite our search by applying the andThen operator >>= as Maybe is an instance of Monad:

findUrlFromSong' :: Song -> Maybe URL
findUrlFromSong' song =
    findAlbum song   >>= \album ->
    findArtist album >>= \artist ->
    findWebSite artist  

or even shorter as we can eliminate the lambda expressions by applying eta-conversion:

findUrlFromSong'' :: Song -> Maybe URL
findUrlFromSong'' song =
    findAlbum song >>= findArtist >>= findWebSite

Using it in GHCi:

ghci> findUrlFromSong'' "All you need is love"
Nothing
ghci> findUrlFromSong'' "An Ending"
Just "http://www.brian-eno.net"

The expression findAlbum song >>= findArtist >>= findWebSite and the sequencing of actions in the pipeline example return str >>= return . length . words >>= return . (3 *) have a similar structure.

But the behaviour of both chains is quite different: In the Maybe Monad a >>= b does not evaluate b if a == Nothing but stops the whole chain of actions by simply returning Nothing.

The pattern matching and 'short-circuiting' is directly coded into the definition of (>>=) in the Monad implementation of Maybe:

instance  Monad Maybe  where
    (Just x) >>= k      = k x
    Nothing  >>= _      = Nothing

This elegant feature of (>>=) in the Maybe Monad allows us to avoid ugly and repetetive coding.

Avoiding partial functions by using Maybe

Maybe is often used to avoid the exposure of partial functions to client code. Take for example division by zero or computing the square root of negative numbers which are undefined (at least for real numbers). Here come safe – that is total – definitions of these functions that return Nothing for undefined cases:

safeRoot :: Double -> Maybe Double
safeRoot x
    | x >= 0    = Just (sqrt x)
    | otherwise = Nothing

safeReciprocal :: Double -> Maybe Double
safeReciprocal x
    | x /= 0    = Just (1/x)
    | otherwise = Nothing

As we have already learned the monadic >>= operator allows to chain such function as in the following example:

safeRootReciprocal :: Double -> Maybe Double
safeRootReciprocal x = return x >>= safeReciprocal >>= safeRoot

This can be written even more terse as:

safeRootReciprocal :: Double -> Maybe Double
safeRootReciprocal = safeReciprocal >=> safeRoot

The use of the Kleisli 'fish' operator >=> makes it more evident that we are actually aiming at a composition of the monadic functions safeReciprocal and safeRoot.

There are many predefined Monads available in the Haskell curated libraries and it's also possible to combine their effects by making use of MonadTransformers. But that's a different story...

Sourcecode for this section

Interpreter → Reader Monad

In computer programming, the interpreter pattern is a design pattern that specifies how to evaluate sentences in a language. The basic idea is to have a class for each symbol (terminal or nonterminal) in a specialized computer language. The syntax tree of a sentence in the language is an instance of the composite pattern and is used to evaluate (interpret) the sentence for a client.

Quoted from Wikipedia

In the section Singleton → Applicative we have already written a simple expression evaluator. From that section it should be obvious how easy the definition of evaluators and interpreters is in functional programming languages.

The main ingredients are:

• Algebraic Data Types (ADT) used to define the expression data type which is to be evaluated
• An evaluator function that uses pattern matching on the expression ADT
• 'implicit' threading of an environment

In the section on Singleton we have seen that some kind of 'implicit' threading of the environment can be already achieved with `Applicative Functors. We still had the environment as an explicit parameter of the eval function:

eval :: Num e => Exp e -> Env e -> e

but we could omit it in the pattern matching equations:

eval (Var x)   = fetch x
eval (Val i)   = pure i
eval (Add p q) = pure (+) <*> eval p  <*> eval q  
eval (Mul p q) = pure (*) <*> eval p  <*> eval q

By using Monads the handling of the environment can be made even more implicit.

I'll demonstrate this with a slightly extended version of the evaluator. In the first step we extend the expression syntax to also provide let expressions and generic support for binary operators:

-- | a simple expression ADT
data Exp a =
      Var String                            -- a variable to be looked up
    | BinOp (BinOperator a) (Exp a) (Exp a) -- a binary operator applied to two expressions
    | Let String (Exp a) (Exp a)            -- a let expression
    | Val a                                 -- an atomic value

-- | a binary operator type
type BinOperator a =  a -> a -> a

-- | the environment is just a list of mappings from variable names to values
type Env a = [(String, a)]

With this data type we can encode expressions like:

let x = 4+5
in 2*x

as:

Let "x" (BinOp (+) (Val 4) (Val 5))
        (BinOp (*) (Val 2) (Var "x"))

In order to evaluate such expression we must be able to modify the environment at runtime to create a binding for the variable x which will be referred to in the in part of the expression.

Next we define an evaluator function that pattern matches the above expression ADT:

eval :: MonadReader (Env a) m => Exp a -> m a
eval (Val i)          = return i
eval (Var x)          = asks (fetch x)
eval (BinOp op e1 e2) = liftM2 op (eval e1) (eval e2)
eval (Let x e1 e2)    = eval e1 >>= \v -> local ((x,v):) (eval e2)

Let's explore this dense code line by line.

eval :: MonadReader (Env a) m => Exp a -> m a

The most simple instance for MonadReader is the partially applied function type ((->) env). Let's assume the compiler will choose this type as the MonadReader instance. We can then rewrite the function signature as follows:

eval :: Exp a -> ((->) (Env a)) a  -- expanding m to ((->) (Env a))
eval :: Exp a -> Env a -> a        -- applying infix notation for (->)

This is exactly the signature we were using for the Applicative eval function which matches our original intent to eval an expression of type Exp a in an environment of type Env a to a result of type a.

eval (Val i)          = return i

In this line we are pattern matching for a (Val i). The atomic value i is returned, that is lifted to a value of the type Env a -> a.

eval (Var x)          = asks (fetch x)

asks is a helper function that applies its argument f :: env -> a (in our case (fetch x) which looks up variable x) to the environment. asks is thus typically used to handle environment lookups:

asks :: (MonadReader env m) => (env -> a) -> m a
asks f = ask >>= return . f

Now to the next line handling the application of a binary operator:

eval (BinOp op e1 e2) = liftM2 op (eval e1) (eval e2)

op is a binary function of type a -> a -> a (typical examples are binary arithmetic functions like +, -, *, /).

We want to apply this operation on the two expressions (eval e1) and (eval e2). As these expressions both are to be executed within the same monadic context we have to use liftM2 to lift op into this context:

-- | Promote a function to a monad, scanning the monadic arguments from
-- left to right.  For example,
--
-- > liftM2 (+) [0,1] [0,2] = [0,2,1,3]
-- > liftM2 (+) (Just 1) Nothing = Nothing
--
liftM2  :: (Monad m) => (a1 -> a2 -> r) -> m a1 -> m a2 -> m r
liftM2 f m1 m2 = do { x1 <- m1; x2 <- m2; return (f x1 x2) }

The last step is the evaluation of Let x e1 e2 expressions like Let "x" (Val 7) (BinOp (+) (Var "x") (Val 5)). To make this work we have to evaluate e1 and extend the environment by a binding of the variable x to the result of that evaluation. Then we have to evaluate e2 in the context of the extended environment:

eval (Let x e1 e2)    = eval e1 >>= \v ->           -- bind the result of (eval e1) to v
                        local ((x,v):) (eval e2)    -- add (x,v) to the env, eval e2 in the extended env

The interesting part here is the helper function local f m which applies f to the environment and then executes m against the (locally) changed environment. Providing a locally modified environment as the scope of the evaluation of e2 is exactly what the let binding intends:

-- | Executes a computation in a modified environment.
local :: (r -> r) -- ^ The function to modify the environment.
        -> m a    -- ^ @Reader@ to run in the modified environment.
        -> m a

instance MonadReader r ((->) r) where
    local f m = m . f

Now we can use eval to evaluate our example expression:

interpreterDemo = do
    putStrLn "Interpreter -> Reader Monad + ADTs + pattern matching"
    let exp1 = Let "x"
                (BinOp (+) (Val 4) (Val 5))
                (BinOp (*) (Val 2) (Var "x"))
    print $ runReader (eval exp1) env

-- an then in GHCi:

> interpreterDemo
18

By virtue of the local function we used MonadReader as if it provided modifiable state. So for many use cases that require only local state modifications its not required to use the somewhat more tricky MonadState.

Writing the interpreter function with a MonadState looks like follows:

eval1 :: (MonadState (Env a) m) => Exp a -> m a
eval1 (Val i)          = return i
eval1 (Var x)          = gets (fetch x)
eval1 (BinOp op e1 e2) = liftM2 op (eval1 e1) (eval1 e2)
eval1 (Let x e1 e2)    = eval1 e1        >>= \v ->
                         modify ((x,v):) >>
                         eval1 e2

This section was inspired by ideas presented in Quick Interpreters with the Reader Monad.

Sourcecode for this section

Aspect Weaving → Monad Transformers

In computing, aspect-oriented programming (AOP) is a programming paradigm that aims to increase modularity by allowing the separation of cross-cutting concerns. It does so by adding additional behavior to existing code (an advice) without modifying the code itself, instead separately specifying which code is modified via a "pointcut" specification, such as "log all function calls when the function's name begins with 'set'". This allows behaviors that are not central to the business logic (such as logging) to be added to a program without cluttering the code, core to the functionality.

Quoted from Wikipedia

Stacking Monads

In section Interpreter -> Reader Monad we specified an Interpreter of a simple expression language by defining a monadic eval function:

eval :: Exp a -> Reader (Env a) a  
eval (Var x)          = asks (fetch x)
eval (Val i)          = return i
eval (BinOp op e1 e2) = liftM2 op (eval e1) (eval e2)
eval (Let x e1 e2) = eval e1 >>= \v -> local ((x,v):) (eval e2)

Using the Reader Monad allows to thread an environment through all recursive calls of eval.

A typical extension to such an interpreter would be to provide a log mechanism that allows tracing of the actual sequence of all performed evaluation steps.

In Haskell the typical way to provide such a log is by means of the Writer Monad.

But how to combine the capabilities of the Reader monad code with those of the Writer monad?

The answer is MonadTransformers: specialized types that allow us to stack two monads into a single one that shares the behavior of both.

In order to stack the Writer monad on top of the Reader we use the transformer type WriterT:

-- adding a logging capability to the expression evaluator
eval :: Show a => Exp a -> WriterT [String] (Reader (Env a)) a
eval (Var x)          = tell ["lookup " ++ x] >> asks (fetch x)
eval (Val i)          = tell [show i] >> return i
eval (BinOp op e1 e2) = tell ["Op"] >> liftM2 op (eval e1) (eval e2)
eval (Let x e1 e2)    = do
    tell ["let " ++ x]
    v <- eval e1
    tell ["in"]
    local ((x,v):) (eval e2)

The signature of eval has been extended by Wrapping WriterT [String] around (Reader (Env a)). This denotes a Monad that combines a Reader (Env a) with a Writer [String]. Writer [String] is a Writer that maintains a list of strings as log.

The resulting Monad supports function of both MonadReader and MonadWriter typeclasses. As you can see in the equation for eval (Var x) we are using MonadWriter.tell for logging and MonadReader.asks for obtaining the environment and compose both monadic actions by >>:

eval (Var x)          = tell ["lookup " ++ x] >> asks (fetch x)

In order to execute this stacked up monads we have to apply the run functions of WriterT and Reader:

ghci> runReader (runWriterT (eval letExp)) [("pi",pi)]
(6.283185307179586,["let x","let y","Op","5.0","7.0","in","Op","lookup y","6.0","in","Op","lookup pi","lookup x"])

For more details on MonadTransformers please have a look at the following tutorials:

MonadTransformers Wikibook

Monad Transformers step by step

Specifying AOP semantics with MonadTransformers

What we have seen so far is that it possible to form Monad stacks that combine the functionality of the Monads involved: In a way a MonadTransformer adds capabilities that are cross-cutting to those of the underlying Monad.

In the following lines I want to show how MonadTransformers can be used to specify the formal semantics of Aspect Oriented Programming. I have taken the example from Mark P. Jones paper The Essence of AspectJ.

An interpreter for MiniPascal

We start by defining a simple imperative language – MiniPascal:

-- | an identifier type
type Id = String

-- | Integer expressions
data IExp = Lit Int
    | IExp :+: IExp
    | IExp :*: IExp
    | IExp :-: IExp
    | IExp :/: IExp
    | IVar Id deriving (Show)

-- | Boolean expressions
data BExp = T
    | F
    | Not BExp
    | BExp :&: BExp
    | BExp :|: BExp
    | IExp :=: IExp
    | IExp :<: IExp deriving (Show)

-- | Staments
data Stmt = Skip        -- no op
    | Id := IExp        -- variable assignment
    | Begin [Stmt]      -- a sequence of statements
    | If BExp Stmt Stmt -- an if statement
    | While BExp Stmt   -- a while loop
    deriving (Show)

With this igredients its possible to write imperative programs like the following while loop that sums up the natural numbers from 1 to 10:

-- an example program: the MiniPascal equivalent of `sum [1..10]`
program :: Stmt
program =
    Begin [
        "total" := Lit 0,
        "count" := Lit 0,
        While (IVar "count" :<: Lit 10)
            (Begin [
                "count" := (IVar "count" :+: Lit 1),
                "total" := (IVar "total" :+: IVar "count")
            ])
    ]

We define the semantics of this language with an interpreter:

-- | the store used for variable assignments
type Store = Map Id Int

-- | evaluate numeric expression.
iexp :: MonadState Store m => IExp -> m Int
iexp (Lit n) = return n
iexp (e1 :+: e2) = liftM2 (+) (iexp e1) (iexp e2)
iexp (e1 :*: e2) = liftM2 (*) (iexp e1) (iexp e2)
iexp (e1 :-: e2) = liftM2 (-) (iexp e1) (iexp e2)
iexp (e1 :/: e2) = liftM2 div (iexp e1) (iexp e2)
iexp (IVar i)    = getVar i

-- | evaluate logic expressions
bexp :: MonadState Store m => BExp -> m Bool
bexp T           = return True
bexp F           = return False
bexp (Not b)     = fmap not (bexp b)
bexp (b1 :&: b2) = liftM2 (&&) (bexp b1) (bexp b2)
bexp (b1 :|: b2) = liftM2 (||) (bexp b1) (bexp b2)
bexp (e1 :=: e2) = liftM2 (==) (iexp e1) (iexp e2)
bexp (e1 :<: e2) = liftM2 (<)  (iexp e1) (iexp e2)

-- | evaluate statements
stmt :: MonadState Store m => Stmt -> m ()
stmt Skip       = return ()
stmt (i := e)   = do x <- iexp e; setVar i x
stmt (Begin ss) = mapM_ stmt ss
stmt (If b t e) = do
    x <- bexp b
    if x then stmt t
         else stmt e
stmt (While b t) = loop
    where loop = do
            x <- bexp b
            when x $ stmt t >> loop

-- | a variable assignments updates the store (which is maintained in the state)
setVar :: (MonadState (Map k a) m, Ord k) => k -> a -> m ()
setVar i x = do
    store <- get
    put (Map.insert i x store)

-- | lookup a variable in the store. return 0 if no value is found
getVar :: MonadState Store m => Id -> m Int
getVar i = do
    s <- get
    case Map.lookup i s of
        Nothing  -> return 0
        (Just v) -> return v

-- | evaluate a statement
run :: Stmt -> Store
run s = execState (stmt s) (Map.fromList [])

-- and then in GHCi:
ghci> run program
fromList [("count",10),("total",55)]

So far this is nothing special, just a minimal interpreter for an imperative language. Side effects in form of variable assignments are modelled with an environment that is maintained in a state monad.

In the next step we want to extend this language with features of aspect oriented programming in the style of AspectJ: join points, point cuts, and advices.

An Interpreter for AspectPascal

To keep things simple we will specify only two types of joint points: variable assignment and variable reading:

data JoinPointDesc = Get Id | Set Id

Get i describes a join point at which the variable i is read, while Set i described a join point at which a value is assigned to the variable i.

Following the concepts of ApectJ pointcut expressions are used to describe sets of join points. The abstract syntax for pointcuts is as follows:

data PointCut = Setter                  -- the pointcut of all join points at which a variable is being set
              | Getter                  -- the pointcut of all join points at which a variable is being read
              | AtVar Id                -- the point cut of all join points at which a the variable is being set or read
              | NotAt PointCut          -- not a
              | PointCut :||: PointCut  -- a or b
              | PointCut :&&: PointCut  -- a and b

For example this syntax can be used to specify the pointcut of all join points at which the variable x is set:

(Setter :&&: AtVar "x")

The following function computes whether a PointCut contains a given JoinPoint:

includes :: PointCut -> (JoinPointDesc -> Bool)
includes Setter     (Set i) = True
includes Getter     (Get i) = True
includes (AtVar i)  (Get j) = i == j
includes (AtVar i)  (Set j) = i == j
includes (NotAt p)  d       = not (includes p d)
includes (p :||: q) d       = includes p d || includes q d
includes (p :&&: q) d       = includes p d && includes q d
includes _ _                = False

In AspectJ aspect oriented extensions to a program are described using the notion of advices. We follow the same design here: each advice includes a pointcut to specify the join points at which the advice should be used, and a statement (in MiniPascal syntax) to specify the action that should be performed at each matching join point.

In AspectPascal we only support two kinds of advice: Before, which will be executed on entry to a join point, and After which will be executed on the exit from a join point:

data Advice = Before PointCut Stmt
            | After  PointCut Stmt

This allows to define Advices like the following:

-- the countSets Advice traces each setting of a variable and increments the counter "countSet"
countSets = After (Setter :&&: NotAt (AtVar "countSet") :&&: NotAt (AtVar "countGet"))
                  ("countSet" := (IVar "countSet" :+: Lit 1))

-- the countGets Advice traces each lookup of a variable and increments the counter "countGet"
countGets = After (Getter :&&: NotAt (AtVar "countSet") :&&: NotAt (AtVar "countGet"))
                  ("countGet" := (IVar "countGet" :+: Lit 1))

The rather laborious PointCut definition is used to select access to all variable apart from countGet and countSet. This is required as the action part of the Advices are normal MiniPascal statements that are executed by the same interpreter as the main program which is to be extended by advices. If those filters were not present execution of those advices would result in non-terminating loops, as the action statements also access variables.

A complete AspectPascal program will now consist of a stmt (the original program) plus a list of advices that should be executed to implement the cross-cutting aspects:

-- | Aspects are just a list of Advices
type Aspects = [Advice]

In order to extend our interpreter to execute additional behaviour decribed in advices we will have to provide all evaluating functions with access to the Aspects. As the Aspects will not be modified at runtime the typical solution would be to provide them by a Reader Aspects monad. We already have learnt that we can use a MonadTransformer to stack our existing State monad with a Reader monad. The respective Transformer is ReaderT. We thus extend the signature of the evaluation functions accordingly, eg:

-- from:
iexp :: MonadState Store m => IExp -> m Int

-- to:
iexp :: MonadState Store m => IExp -> ReaderT Aspects m Int

Apart from extendig the signatures we have to modify all places where variables are accessed to apply the matching advices. So for instance in the equation for iexp (IVar i) we specify that (getVar i) should be executed with applying all advices that match the read access to variable i – that is (Get i) by writing:

iexp (IVar i)    = withAdvice (Get i) (getVar i)

So the complete definition of iexp is:

iexp :: MonadState Store m => IExp -> ReaderT Aspects m Int
iexp (Lit n) = return n
iexp (e1 :+: e2) = liftM2 (+) (iexp e1) (iexp e2)
iexp (e1 :*: e2) = liftM2 (*) (iexp e1) (iexp e2)
iexp (e1 :-: e2) = liftM2 (-) (iexp e1) (iexp e2)
iexp (e1 :/: e2) = liftM2 div (iexp e1) (iexp e2)
iexp (IVar i)    = withAdvice (Get i) (getVar i)

[...] if c is a computation corresponding to some join point with description d, then withAdvice d c wraps the execution of c with the execution of the appropriate Before and After advice, if any:

withAdvice :: MonadState Store m => JoinPointDesc -> ReaderT Aspects m a -> ReaderT Aspects m a
withAdvice d c = do
    aspects <- ask                -- obtaining the Aspects from the Reader monad
    mapM_ stmt (before d aspects) -- execute the statements of all Before advices
    x <- c                        -- execute the actual business logic
    mapM_ stmt (after d aspects)  -- execute the statements of all After advices
    return x

-- collect the statements of Before and After advices matching the join point
before, after :: JoinPointDesc -> Aspects -> [Stmt]
before d as = [s | Before c s <- as, includes c d]
after  d as = [s | After  c s <- as, includes c d]

In the same way the equation for variable assignment stmt (i := e) we specify that (setVar i x) should be executed with applying all advices that match the write access to variable i – that is (Set i) by noting:

stmt (i := e)   = do x <- iexp e; withAdvice (Set i) (setVar i x)

The complete implementation for stmt then looks like follows:

stmt :: MonadState Store m => Stmt -> ReaderT Aspects m ()
stmt Skip       = return ()
stmt (i := e)   = do x <- iexp e; withAdvice (Set i) (setVar i x)
stmt (Begin ss) = mapM_ stmt ss
stmt (If b t e) = do
    x <- bexp b
    if x then stmt t
         else stmt e
stmt (While b t) = loop
    where loop = do
            x <- bexp b
            when x $ stmt t >> loop

Finally we have to extend run function to properly handle the monad stack:

run :: Aspects -> Stmt -> Store
run a s = execState (runReaderT (stmt s) a) (Map.fromList [])

-- and then in GHCi:
ghci> run [] program
fromList [("count",10),("total",55)]

ghci> run [countSets] program
fromList [("count",10),("countSet",22),("total",55)]

ghci> run [countSets, countGets] program
fromList [("count",10),("countGet",41),("countSet",22),("total",55)]

So executing the program with an empty list of advices yields the same result as executing the program with initial interpreter. Once we execute the program with the advices countGets and countSets the resulting map contains values for the variables countGet and countSet which have been incremented by the statements of both advices.

We have utilized Monad Transformers to extend our original interpreter in a minamally invasive way, to provide a formal and executable semantics for a simple aspect-oriented language in the style of AspectJ.

Composite → SemiGroup → Monoid

In software engineering, the composite pattern is a partitioning design pattern. The composite pattern describes a group of objects that is treated the same way as a single instance of the same type of object. The intent of a composite is to "compose" objects into tree structures to represent part-whole hierarchies. Implementing the composite pattern lets clients treat individual objects and compositions uniformly. (Quoted from Wikipedia)

A typical example for the composite pattern is the hierarchical grouping of test cases to TestSuites in a testing framework. Take for instance the following class diagram from the JUnit cooks tour which shows how JUnit applies the Composite pattern to group TestCases to TestSuites while both of them implement the Test interface:

In Haskell we could model this kind of hierachy with an algebraic data type (ADT):

-- the composite data structure: a Test can be either a single TestCase
-- or a TestSuite holding a list of Tests
data Test = TestCase TestCase
          | TestSuite [Test]

-- a test case produces a boolean when executed
type TestCase = () -> Bool

The function run as defined below can either execute a single TestCase or a composite TestSuite:

-- execution of a Test.
run :: Test -> Bool
run (TestCase t)  = t () -- evaluating the TestCase by applying t to ()
run (TestSuite l) = all (True ==) (map run l) -- running all tests in l and return True if all tests pass

-- a few most simple test cases
t1 :: Test
t1 = TestCase (\() -> True)
t2 :: Test
t2 = TestCase (\() -> True)
t3 :: Test
t3 = TestCase (\() -> False)
-- collecting all test cases in a TestSuite
ts = TestSuite [t1,t2,t3]

As run is of type run :: Test -> Bool we can use it to execute single TestCases or complete TestSuites. Let's try it in GHCI:

ghci> run t1
True
ghci> run ts
False

In order to aggregate TestComponents we follow the design of JUnit and define a function addTest. Adding two atomic Tests will result in a TestSuite holding a list with the two Tests. If a Test is added to a TestSuite, the test is added to the list of tests of the suite. Adding TestSuites will merge them.

-- adding Tests
addTest :: Test -> Test -> Test
addTest t1@(TestCase _) t2@(TestCase _)   = TestSuite [t1,t2]
addTest t1@(TestCase _) (TestSuite list)  = TestSuite ([t1] ++ list)
addTest (TestSuite list) t2@(TestCase _)  = TestSuite (list ++ [t2])
addTest (TestSuite l1) (TestSuite l2)     = TestSuite (l1 ++ l2)

If we take a closer look at addTest we will see that it is a associative binary operation on the set of Tests.

In mathemathics a set with an associative binary operation is a Semigroup.

We can thus make our type Test an instance of the type class Semigroup with the following declaration:

instance Semigroup Test where
    (<>)   = addTest

What's not visible from the JUnit class diagram is how typical object oriented implementations will have to deal with null-references. That is the implementations would have to make sure that the methods run and addTest will handle empty references correctly. With Haskells algebraic data types we would rather make this explicit with a dedicated Empty element. Here are the changes we have to add to our code:

-- the composite data structure: a Test can be Empty, a single TestCase
-- or a TestSuite holding a list of Tests
data Test = Empty
          | TestCase TestCase
          | TestSuite [Test]

-- execution of a Test.
run :: Test -> Bool
run Empty         = True -- empty tests will pass
run (TestCase t)  = t () -- evaluating the TestCase by applying t to ()
--run (TestSuite l) = foldr ((&&) . run) True l
run (TestSuite l) = all (True ==) (map run l) -- running all tests in l and return True if all tests pass

-- addTesting Tests
addTest :: Test -> Test -> Test
addTest Empty t                           = t
addTest t Empty                           = t
addTest t1@(TestCase _) t2@(TestCase _)   = TestSuite [t1,t2]
addTest t1@(TestCase _) (TestSuite list)  = TestSuite ([t1] ++ list)
addTest (TestSuite list) t2@(TestCase _)  = TestSuite (list ++ [t2])
addTest (TestSuite l1) (TestSuite l2)     = TestSuite (l1 ++ l2)

From our additions it's obvious that Empty is the identity element of the addTest function. In Algebra a Semigroup with an identity element is called Monoid:

In abstract algebra, [...] a monoid is an algebraic structure with a single associative binary operation and an identity element. Quoted from Wikipedia

With haskell we can declare Test as an instance of the Monoid type class by defining:

instance Monoid Test where
    mempty = Empty

We can now use all functions provided by the Monoid type class to work with our Test:

compositeDemo = do
    print $ run $ t1 <> t2
    print $ run $ t1 <> t2 <> t3

We can also use the function mconcat :: Monoid a => [a] -> a on a list of Tests: mconcat composes a list of Tests into a single Test. That's exactly the mechanism of forming a TestSuite from atomic TestCases.

compositeDemo = do
    print $ run $ mconcat [t1,t2]
    print $ run $ mconcat [t1,t2,t3]

This particular feature of mconcat :: Monoid a => [a] -> a to condense a list of Monoids to a single Monoid can be used to drastically simplify the design of our test framework.

We need just one more hint from our mathematician friends:

Functions are monoids if they return monoids Quoted from blog.ploeh.dk

Currently our TestCases are defined as functions yielding boolean values:

type TestCase = () -> Bool

If Bool was a Monoid we could use mconcat to form test suite aggregates. Bool in itself is not a Monoid; but together with a binary associative operation like (&&) or (||) it will form a Monoid.

The intuitive semantics of a TestSuite is that a whole Suite is "green" only when all enclosed TestCases succeed. That is the conjunction of all TestCases must return True.

So we are looking for the Monoid of boolean values under conjunction (&&). In Haskell this Monoid is called All):

-- | Boolean monoid under conjunction ('&&').
-- >>> getAll (All True <> mempty <> All False)
-- False
-- >>> getAll (mconcat (map (\x -> All (even x)) [2,4,6,7,8]))
-- False
newtype All = All { getAll :: Bool }

instance Semigroup All where
        (<>) = coerce (&&)

instance Monoid All where
        mempty = All True

Making use of All our improved definition of TestCases is as follows:

type SmartTestCase = () -> All

Now our test cases do not directly return a boolean value but an All wrapper, which allows automatic conjunction of test results to a single value. Here are our redefined TestCases:

tc1 :: SmartTestCase
tc1 () = All True
tc2 :: SmartTestCase
tc2 () = All True
tc3 :: SmartTestCase
tc3 () = All False

We now implement a new evaluation function run' which evaluates a SmartTestCase (which may be either an atomic TestCase or a TestSuite assembled by mconcat) to a single boolean result.

run' :: SmartTestCase -> Bool
run' tc = getAll $ tc ()  

This version of run is much simpler than the original and we can completely avoid the rather laborious addTest function. We also don't need any composite type Test. By just sticking to the Haskell built-in type classes we achieve cleanly designed functionality with just a few lines of code.

compositeDemo = do
    -- execute a single test case
    print $ run' tc1

    --- execute a complex test suite
    print $ run' $ mconcat [tc1,tc2]
    print $ run' $ mconcat [tc1,tc2,tc3]

For more details on Composite as a Monoid please refer to the following blog: Composite as Monoid

Sourcecode for this section

Visitor → Foldable

[...] the visitor design pattern is a way of separating an algorithm from an object structure on which it operates. A practical result of this separation is the ability to add new operations to existent object structures without modifying the structures. It is one way to follow the open/closed principle. (Quoted from Wikipedia)

In functional languages - and Haskell in particular - we have a whole armada of tools serving this purpose:

• higher order functions like map, fold, filter and all their variants allow to "visit" lists
• The Haskell type classes Functor, Foldable, Traversable, etc. provide a generic framework to allow visiting any algebraic datatype by just deriving one of these type classes.

Using Foldable

-- we are re-using the Exp data type from the Singleton example
-- and transform it into a Foldable type:
instance Foldable Exp where
    foldMap f (Val x)   = f x
    foldMap f (Add x y) = foldMap f x `mappend` foldMap f y
    foldMap f (Mul x y) = foldMap f x `mappend` foldMap f y

filterF :: Foldable f => (a -> Bool) -> f a -> [a]
filterF p = foldMap (\a -> if p a then [a] else [])

visitorDemo = do
    let exp = Mul (Add (Val 3) (Val 2))
                  (Mul (Val 4) (Val 6))
    putStr "size of exp: "
    print $ length exp
    putStrLn "filter even numbers from tree"
    print $ filterF even exp

By virtue of the instance declaration Exp becomes a Foldable instance an can be used with arbitrary functions defined on Foldable like length in the example.

foldMap can for example be used to write a filtering function filterFthat collects all elements matching a predicate into a list.

Alternative approaches

Visitory as Sum type

Sourcecode for this section

Iterator → Traversable

[...] the iterator pattern is a design pattern in which an iterator is used to traverse a container and access the container's elements. The iterator pattern decouples algorithms from containers; in some cases, algorithms are necessarily container-specific and thus cannot be decoupled. Quoted from Wikipedia

Iterating over a Tree

The most generic type class enabling iteration over algebraic data types is Traversable as it allows combinations of map and fold operations. We are re-using the Exp type from earlier examples to show what's needed for enabling iteration in functional languages.

instance Functor Exp where
    fmap f (Var x)       = Var x
    fmap f (Val a)       = Val $ f a
    fmap f (Add x y)     = Add (fmap f x) (fmap f y)
    fmap f (Mul x y)     = Mul (fmap f x) (fmap f y)

instance Traversable Exp where
    traverse g (Var x)   = pure $ Var x
    traverse g (Val x)   = Val <$> g x
    traverse g (Add x y) = Add <$> traverse g x <*> traverse g y
    traverse g (Mul x y) = Mul <$> traverse g x <*> traverse g y

With this declaration we can traverse an Exp tree:

iteratorDemo = do
    putStrLn "Iterator -> Traversable"
    let exp = Mul (Add (Val 3) (Val 1))
                (Mul (Val 2) (Var "pi"))
        env = [("pi", pi)]
    print $ traverse (\x c -> if even x then [x] else [2*x]) exp 0

In this example we are touching all (nested) Val elements and multiply all odd values by 2.

Combining traversal operations

Compared with Foldable or Functor the declaration of a Traversable instance looks a bit intimidating. In particular the type signature of traverse:

traverse :: (Traversable t, Applicative f) => (a -> f b) -> t a -> f (t b)

looks like quite a bit of over-engineering for simple traversals as in the above example.

In oder to explain the real power of the Traversable type class we will look at a more sophisticated example in this section. This example was taken from the paper The Essence of the Iterator Pattern.

The Unix utility wc is a good example for a traversal operation that performs several different tasks while traversing its input:

echo "counting lines, words and characters in one traversal" | wc
      1       8      54

The output simply means that our input has 1 line, 8 words and a total of 54 characters. Obviously an efficients implementation of wc will accumulate the three counters for lines, words and characters in a single pass of the input and will not run three iterations to compute the three counters separately.

Here is a Java implementation:

private static int[] wordCount(String str) {
    int nl=0, nw=0, nc=0;         // number of lines, number of words, number of characters
    boolean readingWord = false;  // state information for "parsing" words
    for (Character c : asList(str)) {
        nc++;                     // count just any character
        if (c == '\n') {
            nl++;                 // count only newlines
        }
        if (c == ' ' || c == '\n' || c == '\t') {
            readingWord = false;  // when detecting white space, signal end of word
        } else if (readingWord == false) {
            readingWord = true;   // when switching from white space to characters, signal new word
            nw++;                 // increase the word counter only once while in a word
        }
    }
    return new int[]{nl,nw,nc};
}

private static List<Character> asList(String str) {
    return str.chars().mapToObj(c -> (char) c).collect(Collectors.toList());
}

Please note that the for (Character c : asList(str)) {...} notation is just syntactic sugar for

for (Iterator<Character> iter = asList(str).iterator(); iter.hasNext();) {
    Character c = iter.next();
    ...
}

For efficiency reasons this solution may be okay, but from a design perspective the solution lacks clarity as the required logic for accumulating the three counters is heavily entangled within one code block. Just imagine how the complexity of the for-loop will increase once we have to add new features like counting bytes, counting white space or counting maximum line width.

So we would like to be able to isolate the different counting algorithms (separation of concerns) and be able to combine them in a way that provides efficient one-time traversal.

We start with the simple task of character counting:

type Count = Const (Sum Integer)

count :: a -> Count b
count _ = Const 1

cciBody :: Char -> Count a
cciBody = count

cci :: String -> Count [a]
cci = traverse cciBody

-- and then in ghci:
> cci "hello world"
Const (Sum {getSum = 11})

For each character we just emit a Const 1 which are elements of type Const (Sum Integer). As (Sum Integer) is the monoid of Integers under addition, this design allows automatic summation over all collected Const values.

The next step of counting newlines looks similar:

-- return (Sum 1) if true, else (Sum 0)
test :: Bool -> Sum Integer
test b = Sum $ if b then 1 else 0

-- use the test function to emit (Sum 1) only when a newline char is detected
lciBody :: Char -> Count a
lciBody c = Const $ test (c == '\n')

-- define the linecount using traverse
lci :: String -> Count [a]
lci = traverse lciBody

-- and the in ghci:
> lci "hello \n world"
Const (Sum {getSum = 1})

Now let's try to combine character counting and line counting. In order to match the type declaration for traverse:

traverse :: (Traversable t, Applicative f) => (a -> f b) -> t a -> f (t b)

We had to define cciBody and lciBody so that their return types are Applicative Functors. The good news is that the product of two Applicatives is again an Applicative (the same holds true for Composition of Applicatives). With this knowledge we can now use traverse to use the product of cciBody and lciBody:

import Data.Functor.Product             -- Product of Functors

-- define infix operator for building a Functor Product
(<#>) :: (Functor m, Functor n) => (a -> m b) -> (a -> n b) -> (a -> Product m n b)
(f <#> g) y = Pair (f y) (g y)

-- use a single traverse to apply the Product of cciBody and lciBody
clci :: String -> Product Count Count [a]
clci = traverse (cciBody <#> lciBody)

-- and then in ghci:
> clci "hello \n world"
Pair (Const (Sum {getSum = 13})) (Const (Sum {getSum = 1}))

So we have achieved our aim of separating line counting and character counting in separate functions while still being able to apply them in only one traversal.

The only piece missing is the word counting. This is a bit tricky as we can not just increase a counter by looking at each single character but we have to take into account the status of the previously read character as well:

• If the previous character was non-whitespace and the current is also non-whitespace we are still reading the same word and don't increment the word count.
• If the previous character was non-whitespace and the current is a whitespace character the last word was ended but we don't increment the word count.
• If the previous character was whitespace and the current is also whitespace we are still reading whitespace between words and don't increment the word count.
• If the previous character was whitespace and the current is a non-whitespace character the next word has started and we increment the word count.

Keeping track of the state of the last character could be achieved by using a state monad (and wrapping it as an Applicative Functor to make it compatible with traverse). The actual code for this solution is kept in the sourcecode for this section (functions wciBody' and wci' in particular). But as this approach is a bit noisy I'm presenting a simpler solution suggested by Noughtmare.

In his approach we'll define a data structure that will keep track of the changes between whitespace and non-whitespace:

data SepCount = SC Bool Bool Integer
  deriving Show

mkSepCount :: (a -> Bool) -> a -> SepCount
mkSepCount pred x = SC p p (if p then 0 else 1)
  where
    p = pred x

getSepCount :: SepCount -> Integer
getSepCount (SC _ _ n) = n    

We then define the semantics for (<>) which implements the actual bookkeeping needed when mappending two SepCount items:

instance Semigroup SepCount where
  (SC l0 r0 n) <> (SC l1 r1 m) = SC l0 r1 x where
    x | not r0 && not l1 = n + m - 1
      | otherwise = n + m

Based on these definitions we can then implement the wordcounting as follows:

wciBody :: Char -> Const (Maybe SepCount) Integer
wciBody = Const . Just . mkSepCount isSpace where
    isSpace :: Char -> Bool
    isSpace c = c == ' ' || c == '\n' || c == '\t'

-- using traverse to count words in a String
wci :: String -> Const (Maybe SepCount) [Integer]
wci = traverse wciBody 

-- Forming the Product of character counting, line counting and word counting
-- and performing a one go traversal using this Functor product
clwci :: String -> (Product (Product Count Count) (Const (Maybe SepCount))) [Integer]
clwci = traverse (cciBody <#> lciBody <#> wciBody)  

-- extracting the actual Integer value from a `Const (Maybe SepCount) a` expression 
extractCount :: Const (Maybe SepCount) a -> Integer
extractCount (Const (Just sepCount)) =  getSepCount sepCount  

-- the actual wordcount implementation.
-- for any String a triple of linecount, wordcount, charactercount is returned
wc :: String -> (Integer, Integer, Integer)
wc str =
    let raw = clwci str
        cc  = coerce $ pfst (pfst raw)
        lc  = coerce $ psnd (pfst raw)
        wc  = extractCount  (psnd raw)
    in (lc,wc,cc)

This sections was meant to motivate the usage of the Traversable type. Of course the word count example could be solved in much simpler ways. Here is one solution suggested by NoughtMare.

We simply use foldMap to perform a map / reduce based on our already defined cciBody, lciBody and wciBody functions. As clwci'' now returns a simple tuple instead of the more clumsy Product type also the final wordcound function wc'' now looks way simpler:

clwci'' :: Foldable t => t Char -> (Count [a], Count [a], Const (Maybe SepCount) Integer)
clwci'' = foldMap (\x -> (cciBody x,  lciBody x, wciBody x))

wc'' :: String -> (Integer, Integer, Integer)
wc'' str =
    let (rawCC, rawLC, rawWC) = clwci'' str
        cc  = coerce rawCC
        lc  = coerce rawLC
        wc  = extractCount rawWC
    in (lc,wc,cc)    

As map / reduce with foldMap is such a powerful tool I've written a dedicated section on this topic further down in this study.

Sourcecode for this section

The Pattern behind the Patterns → Category

If you've ever used Unix pipes, you'll understand the importance and flexibility of composing small reusable programs to get powerful and emergent behaviors. Similarly, if you program functionally, you'll know how cool it is to compose a bunch of small reusable functions into a fully featured program.

Category theory codifies this compositional style into a design pattern, the category. Quoted from HaskellForAll

In most of the patterns and type classes discussed so far we have seen a common theme: providing means to compose behaviour and structure is one of the most important tools to design complex software by combining simpler components.

Function Composition

Function composition is a powerful and elegant tool to compose complex functionality out of simpler building blocks. We already have seen several examples of it in the course of this study. Functions can be composed by using the binary (.) operator:

ghci> :type (.)
(.) :: (b -> c) -> (a -> b) -> a -> c

It is defined as:

(f . g) x = f (g x)

This operator can be used to combine simple functions to awesome one-liners (and of course much more useful stuff):

ghci> product . filter odd . map length . words . reverse $ "function composition is awesome"
77

Function composition is associative (f . g) . h = f . (g . h):

ghci> (((^2) . length) . words) "hello world"
4
ghci> ((^2) . (length . words)) "hello world"
4

And composition has a neutral (or identity) element id so that f . id = id . f:

ghci> (length . id) [1,2,3]
3
ghci> (id . length) [1,2,3]
3

The definitions of (.) and id plus the laws of associativity and identity match exactly the definition of a category:

In mathematics, a category [...] is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object.

Quoted from Wikipedia

In Haskell a category is defined as as a type class:

class Category cat where
    -- | the identity morphism
    id :: cat a a

    -- | morphism composition
    (.) :: cat b c -> cat a b -> cat a c

Please note: The name Category may be a bit misleading, since this type class cannot represent arbitrary categories, but only categories whose objects are objects of Hask, the category of Haskell types.

Instances of Category should satisfy that (.) and id form a Monoid – that is id should be the identity of (.) and (.) should be associative:

f  . id      =  f            -- (right identity)
id . f       =  f            -- (left identity)
f . (g . h)  =  (f . g) . h  -- (associativity)

As function composition fulfills these category laws the function type constructor (->) can be defined as an instance of the category type class:

instance Category (->) where
    id  = GHC.Base.id
    (.) = (GHC.Base..)

Monadic Composition

In the section on the Maybe Monad we have seen that monadic operations can be chained with the Kleisli operator >=>:

safeRoot           :: Double -> Maybe Double
safeRoot x
    | x >= 0    = Just (sqrt x)
    | otherwise = Nothing

safeReciprocal     :: Double -> Maybe Double
safeReciprocal x
    | x /= 0    = Just (1/x)
    | otherwise = Nothing

safeRootReciprocal :: Double -> Maybe Double
safeRootReciprocal = safeReciprocal >=> safeRoot

The operator <=< just flips the arguments of >=> and thus provides right-to-left composition. When we compare the signature of <=< with the signature of . we notice the similarity of both concepts:

(.)   ::            (b ->   c) -> (a ->   b) -> a ->   c
(<=<) :: Monad m => (b -> m c) -> (a -> m b) -> a -> m c

Even the implementation of <=< is quite similar to the definition of .

(f  .  g) x = f     (g x)
(f <=< g) x = f =<< (g x)

The essential diffenerce is that <=< maintains a monadic structure when producing its result.

Next we compare signatures of id and its monadic counterpart return:

id     ::              (a ->   a)
return :: (Monad m) => (a -> m a)

Here again return always produces a monadic structure.

So the category for Monads can simply be defined as:

-- | Kleisli arrows of a monad.
newtype Kleisli m a b = Kleisli { runKleisli :: a -> m b }

instance Monad m => Category (Kleisli m) where
    id = Kleisli return
    (Kleisli f) . (Kleisli g) = Kleisli (f <=< g)

So if monadic actions form a category we expect that the law of identity and associativity hold:

return <=< f    = f                -- left identity

f <=< return    = f                -- right identity

(f <=< g) <=< h = f <=< (g <=< h)  -- associativity

Let's try to prove it by applying some equational reasoning. First we take the definition of <=<: (f <=< g) x = f =<< (g x) to expand the above equations:

-- 1. left identity
return <=< f     = f    -- left identity (to be proven)
(return <=< f) x = f x  -- eta expand
return =<< (f x) = f x  -- expand <=< by above definition
return =<< f     = f    -- eta reduce
f >>= return     = f    -- replace =<< with >>= and flip arguments


-- 2 right identity
f <=< return     = f    -- right identity (to be proven)
(f <=< return) x = f x  -- eta expand
f =<< (return x) = f x  -- expand <=< by above definition
return x >>= f   = f x  -- replace =<< with >>= and flip arguments

-- 3. associativity
(f <=< g) <=< h             = f <=< (g <=< h)  -- associativity (to be proven)
((f <=< g) <=< h) x         = (f <=< (g <=< h)) x -- eta expand
(f <=< g) =<< (h x)         = f =<< ((g <=< h) x) -- expand outer <=< on both sides
(\y -> (f <=< g) y) =<< h x = f =<< ((g <=< h) x) -- eta expand on left hand side
(\y -> f =<< (g y)) =<< h x = f =<< ((g <=< h) x) -- expand inner <=< on the lhs
(\y -> f =<< (g y)) =<< h x = f =<< (g =<< (h x)) -- expand inner <=< on the rhs
h x >>= (\y -> f =<< (g y)) = f =<< (g =<< (h x)) -- replace outer =<< with >>= and flip arguments on lhs
h x >>= (\y -> g y >>= f)   = f =<< (g =<< (h x)) -- replace inner =<< with >>= and flip arguments on lhs
h x >>= (\y -> g y >>= f)   = (g =<< (h x)) >>= f -- replace outer =<< with >>= and flip arguments on rhs
h x >>= (\y -> g y >>= f)   = ((h x) >>= g) >>= f -- replace inner =<< with >>= and flip arguments on rhs
h >>= (\y -> g y >>= f)     = (h >>= g) >>= f     -- eta reduce

So we have transformed our three formulas to the following form:

f >>= return   = f

return x >>= f = f x

h >>= (\y -> g y >>= f)  =  (h >>= g) >>= f

These three equations are equivalent to the Monad Laws, which all Monad instances are required to satisfy:

m >>= return    =  m

return a >>= k  =  k a

m >>= (\x -> k x >>= h)  =  (m >>= k) >>= h

So by virtue of this equivalence any Monad that satisfies the Monad laws automatically satisfies the Category laws.

If you have ever wondered where those monad laws came from, now you know! They are just the category laws in disguise. Consequently, every new Monad we define gives us a category for free!

Quoted from The Category Design Pattern

Conclusion

Category theory codifies [the] compositional style into a design pattern, the category. Moreover, category theory gives us a precise prescription for how to create our own abstractions that follow this design pattern: the category laws. These laws differentiate category theory from other design patterns by providing rigorous criteria for what does and does not qualify as compositional.

One could easily dismiss this compositional ideal as just that: an ideal, something unsuitable for "real-world" scenarios. However, the theory behind category theory provides the meat that shows that this compositional ideal appears everywhere and can rise to the challenge of > messy problems and complex business logic.

Quoted from The Category Design Pattern

Fluent Api → Comonad

In software engineering, a fluent interface [...] is a method for designing object oriented APIs based extensively on method chaining with the goal of making the readability of the source code close to that of ordinary written prose, essentially creating a domain-specific language within the interface.

Quoted from Wikipedia

The Builder Pattern is a typical example for a fluent API. The following short Java snippet show the essential elements:

• creating a builder instance
• invoking a sequence of mutators with... on the builder instance
• finally calling build() to let the Builder create an object

ConfigBuilder builder = new ConfigBuilder();
Config config = builder
        .withProfiling()        // Add profiling
        .withOptimization()     // Add optimization
        .build();
}

The interesting point is that all the with... methods are not implemented as void method but instead all return the Builder instance, which thus allows to fluently chain the next with... call.

Let's try to recreate this fluent chaining of calls in Haskell. We start with a configuration type Config that represents a set of option strings (Options):

type Options = [String]

newtype Config = Conf Options deriving (Show)

Next we define a function configBuilder which takes Options as input and returns a Config instance:

configBuilder :: Options -> Config
configBuilder options = Conf options

-- we can use this to construct a Config instance from a list of Option strings:
ghci> configBuilder ["-O2", "-prof"]
Conf ["-O2","-prof"]

In order to allow chaining of the with... functions they always must return a new Options -> Config function. So for example withProfiling would have the following signature:

withProfiling :: (Options -> Config) -> (Options -> Config)

This signature is straightforward but the implementation needs some thinking: we take a function builder of type Options -> Config as input and must return a new function of the same type that will use the same builder but will add profiling options to the Options parameter opts:

withProfiling builder = \opts -> builder (opts ++ ["-prof", "-auto-all"])

HLint tells us that this can be written more terse as:

withProfiling builder opts = builder (opts ++ ["-prof", "-auto-all"])

In order to keep notation dense we introduce a type alias for the function type Options -> Config:

type ConfigBuilder = Options -> Config

With this shortcut we can implement the other with... functions as:

withWarnings :: ConfigBuilder -> ConfigBuilder
withWarnings builder opts = builder (opts ++ ["-Wall"])

withOptimization :: ConfigBuilder -> ConfigBuilder
withOptimization builder opts = builder (opts ++ ["-O2"])

withLogging :: ConfigBuilder -> ConfigBuilder
withLogging builder opts = builder (opts ++ ["-logall"])

The build() function is also quite straightforward. It constructs the actual Config instance by invoking a given ConfigBuilder on an empty list:

build :: ConfigBuilder -> Config
build builder = builder mempty

-- now we can use it in ghci:
ghci> print (build (withOptimization (withProfiling configBuilder)))
Conf ["-O2","-prof","-auto-all"]

This does not yet look quite object oriented but with a tiny tweak we'll get quite close. We introduce a special operator # that allows to write functional expression in an object-oriented style:

(#) :: a -> (a -> b) -> b
x # f = f x
infixl 0 #

With this operator we can write the above example as:

config = configBuilder
    # withProfiling    -- add profiling
    # withOptimization -- add optimizations
    # build

So far so good. But what does this have to do with Comonads? In the following I'll demonstrate how the chaining of functions as shown in our ConfigBuilder example follows a pattern that is covered by the Comonad type class.

Let's have a second look at the with* functions:

withWarnings :: ConfigBuilder -> ConfigBuilder
withWarnings builder opts = builder (opts ++ ["-Wall"])

withProfiling :: ConfigBuilder -> ConfigBuilder
withProfiling builder opts = builder (opts ++ ["-prof", "-auto-all"])

These functions all are containing code for explicitely concatenating the opts argument with additional Options. In order to reduce repetitive coding we are looking for a way to factor out the concrete concatenation of Options. Going this route the with* function could be rewritten as follows:

withWarnings'' :: ConfigBuilder -> ConfigBuilder
withWarnings'' builder = extend' builder ["-Wall"]

withProfiling'' :: ConfigBuilder -> ConfigBuilder
withProfiling'' builder = extend' builder ["-prof", "-auto-all"]

Here extend' is a higher order function that takes a ConfigBuilder and an Options argument (opts2) and returns a new function that returns a new ConfigBuilder that concatenates its input opts1 with the original opts2 arguments:

extend' :: ConfigBuilder -> Options -> ConfigBuilder
extend' builder opts2 = \opts1 -> builder (opts1 ++ opts2)
-- or even denser without explicit lambda:
extend' builder opts2 opts1 = builder (opts1 ++ opts2)

We could carry this idea of refactoring repetitive code even further by eliminating the extend' from the with* functions. Of course this will change the signature of the functions:

withWarnings' :: ConfigBuilder -> Config
withWarnings' builder = builder ["-Wall"]

withProfiling' :: ConfigBuilder -> Config
withProfiling' builder = builder ["-prof", "-auto-all"]

In order to form fluent sequences of such function calls we need an improved version of the extend function which transparently handles the concatenation of Option arguments and also keeps the chain of with* functions open for the next with* function being applied:

extend'' :: (ConfigBuilder -> Config) -> ConfigBuilder -> ConfigBuilder
extend'' withFun builder opt2 = withFun (\opt1 -> builder (opt1 ++ opt2))

In order to use extend'' efficiently in user code we have to modify our # operator slightly to transparently handle the extending of ConfigBuilder instances when chaining functions of type ConfigBuilder -> Config:

(#>>) :: ConfigBuilder -> (ConfigBuilder -> Config) -> ConfigBuilder
x #>> f = extend'' f x
infixl 0 #>>

User code would then look like follows:

configBuilder
    #>> withProfiling'
    #>> withOptimization'
    #>> withLogging'
    # build
    # print

Now let's have a look at the definition of the Comonad type class. Being the dual of Monad it defines two functions extract and extend which are the duals of return and (>>=):

class Functor w => Comonad w where
    extract :: w a -> a
    extend  :: (w a -> b) -> w a -> w b

With the knowledge that ((->) a) is an instance of Functor we can define a Comonad instance for ((->) Options):

instance {-# OVERLAPPING #-} Comonad ((->) Options) where
    extract :: (Options -> config) -> config
    extract builder = builder mempty
    extend :: ((Options -> config) -> config') ->  (Options -> config) -> (Options -> config')
    extend withFun builder opt2 = withFun (\opt1 -> builder (opt1 ++ opt2))

Now let's again look at the functions build and extend'':

build :: (Options -> Config) -> Config
build builder = builder mempty

extend'' :: ((Options -> Config) -> Config) -> (Options -> Config) -> (Options -> Config)
extend'' withFun builder opt2 = withFun (\opt1 -> builder (opt1 ++ opt2))

It's obvious that build and extract are equivalent as well as extend'' and extend. So we have been inventing a Comonad without knowing about it.

But we are even more lucky! Our Options type (being just a synonym for [String]) together with the concatenation operator (++) forms a Monoid. And for any Monoid m ((->) m) is a Comonad:

instance Monoid m => Comonad ((->) m)  -- as defined in Control.Comonad

So we don't have to define our own instance of Comonad but can rely on the predefined and more generic ((->) m).

Equipped with this knowledge we define a more generic version of our #>> chaining operator:

(#>) :: Comonad w => w a -> (w a -> b) -> w b
x #> f = extend f x
infixl 0 #>

Based on this definition we can finally rewrite the user code as follows

    configBuilder
        #> withProfiling'
        #> withOptimization'
        #> withLogging'
        # extract  -- # build would be fine as well
        # print

This section is based on examples from You could have invented Comonads. Please also check this blogpost which comments on the notion of comonads as objects in Gabriel Gonzales original posting.

Sourcecode for this section.

Beyond type class patterns

The patterns presented in this chapter don't have a direct correspondence to specific type classes. They rather map to more general concepts of functional programming.

Dependency Injection → Parameter Binding, Partial Application

[...] Dependency injection is a technique whereby one object (or static method) supplies the dependencies of another object. A dependency is an object that can be used (a service). An injection is the passing of a dependency to a dependent object (a client) that would use it. The service is made part of the client's state. Passing the service to the client, rather than allowing a client to build or find the service, is the fundamental requirement of the pattern.

This fundamental requirement means that using values (services) produced within the class from new or static methods is prohibited. The client should accept values passed in from outside. This allows the client to make acquiring dependencies someone else's problem. (Quoted from Wikipedia)

In functional languages this is achieved by binding the formal parameters of a function to values.

Let's see how this works in a real world example. Say we have been building a renderer that allows to produce a markdown representation of a data type that represents the table of contents of a document:

-- | a table of contents consists of a heading and a list of entries
data TableOfContents = Section Heading [TocEntry]

-- | a ToC entry can be a heading or a sub-table of contents
data TocEntry = Head Heading | Sub TableOfContents

-- | a heading can be just a title string or an url with a title and the actual link
data Heading = Title String | Url String String

-- | render a ToC entry as a Markdown String with the proper indentation
teToMd :: Int -> TocEntry -> String
teToMd depth (Head head) = headToMd depth head
teToMd depth (Sub toc)   = tocToMd  depth toc

-- | render a heading as a Markdown String with the proper indentation
headToMd :: Int -> Heading -> String
headToMd depth (Title str)     = indent depth ++ "* " ++ str ++ "\n"
headToMd depth (Url title url) = indent depth ++ "* [" ++ title ++ "](" ++ url ++ ")\n"

-- | convert a ToC to Markdown String. The parameter depth is used for proper indentation.
tocToMd :: Int -> TableOfContents -> String
tocToMd depth (Section heading entries) = headToMd depth heading ++ concatMap (teToMd (depth+2)) entries

-- | produce a String of length n, consisting only of blanks
indent :: Int -> String
indent n = replicate n ' '

-- | render a ToC as a Text (consisting of properly indented Markdown)
tocToMDText :: TableOfContents -> T.Text
tocToMDText = T.pack . tocToMd 0

We can use these definitions to create a table of contents data structure and to render it to markdown syntax:

demoDI = do
    let toc = Section (Title "Chapter 1")
                [ Sub $ Section (Title "Section a")
                    [Head $ Title "First Heading",
                     Head $ Url "Second Heading" "http://the.url"]
                , Sub $ Section (Url "Section b" "http://the.section.b.url")
                    [ Sub $ Section (Title "UnderSection b1")
                        [Head $ Title "First", Head $ Title "Second"]]]
    putStrLn $ T.unpack $ tocToMDText toc

-- and the in ghci:
ghci > demoDI
* Chapter 1
  * Section a
    * First Heading
    * [Second Heading](http://the.url)
  * [Section b](http://the.section.b.url)
    * UnderSection b1
      * First
      * Second

So far so good. But of course we also want to be able to render our TableOfContent to HTML. As we don't want to repeat all the coding work for HTML we think about using an existing Markdown library.

But we don't want any hard coded dependencies to a specific library in our code.

With these design ideas in mind we specify a rendering processor:

-- | render a ToC as a Text with html markup.
--   we specify this function as a chain of parse and rendering functions
--   which must be provided externally
tocToHtmlText :: (TableOfContents -> T.Text) -- 1. a renderer function from ToC to Text with markdown markups
              -> (T.Text -> MarkDown)        -- 2. a parser function from Text to a MarkDown document
              -> (MarkDown -> HTML)          -- 3. a renderer function from MarkDown to an HTML document
              -> (HTML -> T.Text)            -- 4. a renderer function from HTML to Text
              -> TableOfContents             -- the actual ToC to be rendered
              -> T.Text                      -- the Text output (containing html markup)
tocToHtmlText tocToMdText textToMd mdToHtml htmlToText =
    tocToMdText >>>    -- 1. render a ToC as a Text (consisting of properly indented Markdown)
    textToMd    >>>    -- 2. parse text with Markdown to a MarkDown data structure
    mdToHtml    >>>    -- 3. convert the MarkDown data to an HTML data structure
    htmlToText         -- 4. render the HTML data to a Text with hmtl markup

The idea is simple:

1. We render our TableOfContents to a Markdown Text (e.g. using our already defined tocToMDText function).
2. This text is then parsed into a MarkDown data structure.
3. The Markdown document is rendered into an HTML data structure,
4. which is then rendered to a Text containing html markup.

To notate the chaining of functions in their natural order I have used the >>> operator from Control.Arrow which is defined as follows:

f >>> g = g . f

So >>> is just left to right composition of functions which makes reading of longer composition chains much easier to read (at least for people trained to read from left to right).

Please note that at this point we have not defined the types HTML and Markdown. They are just abstract placeholders and we just expect them to be provided externally. In the same way we just specified that there must be functions available that can be bound to the formal parameters tocToText, textToMd, mdToHtml and htmlToText.

If such functions are avaliable we can inject them (or rather bind them to the formal parameters) as in the following definition:

-- | a default implementation of a ToC to html Text renderer.
--   this function is constructed by partially applying `tocToHtmlText` to four functions
--   matching the signature of `tocToHtmlText`.
defaultTocToHtmlText :: TableOfContents -> T.Text
defaultTocToHtmlText =
    tocToHtmlText
        tocToMDText         -- the ToC to markdown Text renderer as defined above
        textToMarkDown      -- a MarkDown parser, externally provided via import
        markDownToHtml      -- a MarkDown to HTML renderer, externally provided via import
        htmlToText          -- a HTML to Text with html markup, externally provided via import

This definition assumes that apart from tocToMDText which has already been defined the functions textToMarkDown, markDownToHtml and htmlToText are also present in the current scope. This is achieved by the following import statement:

import CheapskateRenderer (HTML, MarkDown, textToMarkDown, markDownToHtml, htmlToText)

The implementation in file CheapskateRenderer.hs then looks like follows:

module CheapskateRenderer where
import qualified Cheapskate                      as C
import qualified Data.Text                       as T
import qualified Text.Blaze.Html                 as H
import qualified Text.Blaze.Html.Renderer.Pretty as R

-- | a type synonym that hides the Cheapskate internal Doc type
type MarkDown = C.Doc

-- | a type synonym the hides the Blaze.Html internal Html type
type HTML = H.Html

-- | parse Markdown from a Text (with markdown markup). Using the Cheapskate library.
textToMarkDown :: T.Text -> MarkDown
textToMarkDown = C.markdown C.def

-- | convert MarkDown to HTML by using the Blaze.Html library
markDownToHtml :: MarkDown -> HTML
markDownToHtml = H.toHtml

-- | rendering a Text with html markup from HTML. Using Blaze again.
htmlToText :: HTML -> T.Text
htmlToText = T.pack . R.renderHtml

Now let's try it out:

demoDI = do
    let toc = Section (Title "Chapter 1")
                [ Sub $ Section (Title "Section a")
                    [Head $ Title "First Heading",
                     Head $ Url "Second Heading" "http://the.url"]
                , Sub $ Section (Url "Section b" "http://the.section.b.url")
                    [ Sub $ Section (Title "UnderSection b1")
                        [Head $ Title "First", Head $ Title "Second"]]]

    putStrLn $ T.unpack $ tocToMDText toc

    putStrLn $ T.unpack $ defaultTocToHtmlText toc  

-- using this in ghci:
ghci > demoDI
* Chapter 1
  * Section a
    * First Heading
    * [Second Heading](http://the.url)
  * [Section b](http://the.section.b.url)
    * UnderSection b1
      * First
      * Second

<ul>
<li>Chapter 1
<ul>
<li>Section a
<ul>
<li>First Heading</li>
<li><a href="http://the.url">Second Heading</a></li>
</ul></li>
<li><a href="http://the.section.b.url">Section b</a>
<ul>
<li>UnderSection b1
<ul>
<li>First</li>
<li>Second</li>
</ul></li>
</ul></li>
</ul></li>
</ul>

By inlining this output into the present Markdown document we can see that Markdown and HTML rendering produce the same structure:

• Chapter 1
  • Section a
    • First Heading
    • Second Heading
  • Section b
    • UnderSection b1
      • First
      • Second

• Chapter 1
  • Section a
    • First Heading
    • Second Heading
  • Section b
    • UnderSection b1
      • First
      • Second

Sourcecode for this section

Alternative approaches to dependency injection

Since the carefree handling of dependencies is an important issue in almost every real-world application, it is not surprising that many different solution patterns have been developed for this over time.

Specifically in the Haskell environment, interesting approaches have been developed, such as

• the use of the Reader Monad
• the use of implicit parameters

I will not go into these approaches further here, as there is already a very detailed description available: Who still uses ReaderT.

There is a controversial discussion about implicit parameters, so I would like to refer to this blog post, which discusses some of those issues.

ComCmand → Functions as First Class Citizens

In object-oriented programming, the command pattern is a behavioral design pattern in which an object is used to encapsulate all information needed to perform an action or trigger an event at a later time. This information includes the method name, the object that owns the method and values for the method parameters.

Quoted from Wikipedia

The Wikipedia article features implementation of a simple example in several languages. I'm quoting the Java version here:

import java.util.ArrayList;

/** The Command interface */
public interface Command {
   void execute();
}

/** The Invoker class */
public class Switch {
   private final ArrayList<Command> history = new ArrayList<>();

   public void storeAndExecute(Command cmd) {
      this.history.add(cmd);
      cmd.execute();
   }
}

/** The Receiver class */
public class Light {
   public void turnOn() {
      System.out.println("The light is on");
   }

   public void turnOff() {
      System.out.println("The light is off");
   }
}

/** The Command for turning on the light - ConcreteCommand #1 */
public class FlipUpCommand implements Command {
   private final Light light;

   public FlipUpCommand(Light light) {
      this.light = light;
   }

   @Override    // Command
   public void execute() {
      light.turnOn();
   }
}

/** The Command for turning off the light - ConcreteCommand #2 */
public class FlipDownCommand implements Command {
   private final Light light;

   public FlipDownCommand(Light light) {
      this.light = light;
   }

   @Override    // Command
   public void execute() {
      light.turnOff();
   }
}

/* The test class or client */
public class PressSwitch {
   public static void main(final String[] arguments){
      // Check number of arguments
      if (arguments.length != 1) {
         System.err.println("Argument \"ON\" or \"OFF\" is required!");
         System.exit(-1);
      }

      Light lamp = new Light();

      Command switchUp = new FlipUpCommand(lamp);
      Command switchDown = new FlipDownCommand(lamp);

      Switch mySwitch = new Switch();

      switch(arguments[0]) {
         case "ON":
            mySwitch.storeAndExecute(switchUp);
            break;
         case "OFF":
            mySwitch.storeAndExecute(switchDown);
            break;
         default:
            System.err.println("Argument \"ON\" or \"OFF\" is required.");
            System.exit(-1);
      }
   }
}

Rewriting this in Haskell is much denser:

import           Control.Monad.Writer  -- the writer monad is used to implement the history

-- The Light data type with two nullary operations to turn the light on or off 
data Light = Light {
      turnOn  :: IO String
    , turnOff :: IO String
}

-- our default instance of a Light
simpleLamp = Light { 
      turnOn  = putStrLn "The Light is on"  >> return "on"
    , turnOff = putStrLn "The Light is off" >> return "off"
}

-- a command to flip on a Light
flipUpCommand :: Light -> IO String
flipUpCommand = turnOn

-- a command to flipDown a Light
flipDownCommand :: Light -> IO String
flipDownCommand = turnOff

-- execute a command and log it
storeAndExecute :: IO String -> WriterT[String] IO ()
storeAndExecute command = do
    logEntry <- liftIO command
    tell [logEntry]
  
commandDemo :: IO ()
commandDemo = do
    let lamp = simpleLamp
    result <- execWriterT $
        storeAndExecute (flipUpCommand lamp)   >>
        storeAndExecute (flipDownCommand lamp) >>
        storeAndExecute (flipUpCommand lamp)

    putStrLn $ "switch history: " ++ show result

Sourcecode for this section

Adapter → Function Composition

"The adapter pattern is a software design pattern (also known as wrapper, an alternative naming shared with the decorator pattern) that allows the interface of an existing class to be used as another interface. It is often used to make existing classes work with others without modifying their source code." (Quoted from Wikipedia

An example is an adapter that converts the interface of a Document Object Model of an XML document into a tree structure that can be displayed.

What does an adapter do? It translates a call to the adapter into a call of the adapted backend code. Which may also involve translation of the argument data.

Say we have some backend function that we want to provide with an adapter. we assume that backend has type c -> d:

backend :: c -> d

Our adapter should be of type a -> b:

adapter :: a -> b

In order to write this adapter we have to write two function. The first is:

marshal :: a -> c

which translated the input argument of adapter into the correct type c that can be digested by the backend. And the second function is:

unmarshal :: d -> b

which translates the result of the backendfunction into the correct return type of adapter. adapter will then look like follows:

adapter :: a -> b
adapter = unmarshal . backend . marshal

So in essence the Adapter Patterns is just function composition.

Here is a simple example. Say we have a backend that understands only 24 hour arithmetics (eg. 23:50 + 0:20 = 0:10).

But in our frontend we don't want to see this ugly arithmetics and want to be able to add minutes to a time representation in minutes (eg. 100 + 200 = 300).

We solve this by using the above mentioned function composition of unmarshal . backend . marshal:

-- a 24:00 hour clock representation of time
newtype WallTime = WallTime (Int, Int) deriving (Show)

-- this is our backend. It can add minutes to a WallTime representation
addMinutesToWallTime :: Int -> WallTime -> WallTime
addMinutesToWallTime x (WallTime (h, m)) =
    let (hAdd, mAdd) = x `quotRem` 60
        hNew = h + hAdd
        mNew = m + mAdd
    in if mNew >= 60
        then
            let (dnew, hnew') = (hNew + 1) `quotRem` 24
            in  WallTime (24*dnew + hnew', mNew-60)
        else WallTime (hNew, mNew)

-- this is our time representation in Minutes that we want to use in the frontend
newtype Minute = Minute Int deriving (Show)

-- convert a Minute value into a WallTime representation
marshalMW :: Minute -> WallTime
marshalMW (Minute x) =
    let (h,m) = x `quotRem` 60
    in WallTime (h `rem` 24, m)

-- convert a WallTime value back to Minutes
unmarshalWM :: WallTime -> Minute
unmarshalWM (WallTime (h,m)) = Minute $ 60 * h + m

-- this is our frontend that add Minutes to a time of a day
-- measured in minutes
addMinutesAdapter :: Int -> Minute -> Minute
addMinutesAdapter x = unmarshalWM . addMinutesToWallTime x . marshalMW

adapterDemo = do
    putStrLn "Adapter vs. function composition"
    print $ addMinutesAdapter 100 $ Minute 400
    putStrLn ""

Sourcecode for this section

Template Method → type class default functions

In software engineering, the template method pattern is a behavioral design pattern that defines the program skeleton of an algorithm in an operation, deferring some steps to subclasses. It lets one redefine certain steps of an algorithm without changing the algorithm's structure. Quoted from Wikipedia

The TemplateMethod pattern is quite similar to the StrategyPattern. The main difference is the level of granularity. In Strategy a complete block of functionality - the Strategy - can be replaced. In TemplateMethod the overall layout of an algorithm is predefined and only specific parts of it may be replaced.

In functional programming the answer to this kind of problem is again the usage of higher order functions.

In the following example we come back to the example for the Adapter. The function addMinutesAdapter lays out a structure for interfacing to some kind of backend:

1. marshalling the arguments into the backend format
2. apply the backend logic to the marshalled arguments
3. unmarshal the backend result data into the frontend format

addMinutesAdapter :: Int -> Minute -> Minute
addMinutesAdapter x = unmarshalWM . addMinutesToWallTime x . marshalMW

In this code the backend functionality - addMinutesToWallTime - is a hardcoded part of the overall structure.

Let's assume we want to use different kind of backend implementations - for instance a mock replacement. In this case we would like to keep the overall structure - the template - and would just make a specific part of it flexible. This sounds like an ideal candidate for the TemplateMethod pattern:

addMinutesTemplate :: (Int -> WallTime -> WallTime) -> Int -> Minute -> Minute
addMinutesTemplate f x =
    unmarshalWM .
    f x .
    marshalMW

addMinutesTemplate has an additional parameter f of type (Int -> WallTime -> WallTime). This parameter may be bound to addMinutesToWallTime or alternative implementations:

-- implements linear addition (the normal case) even for values > 1440
linearTimeAdd :: Int -> Minute -> Minute
linearTimeAdd = addMinutesTemplate addMinutesToWallTime

-- implements cyclic addition, respecting a 24 hour (1440 Min) cycle
cyclicTimeAdd :: Int -> Minute -> Minute
cyclicTimeAdd = addMinutesTemplate addMinutesToWallTime'

where addMinutesToWallTime' implements a silly 24 hour cyclic addition:

-- a 24 hour (1440 min) cyclic version of addition: 1400 + 100 = 60
addMinutesToWallTime' :: Int -> WallTime -> WallTime
addMinutesToWallTime' x (WallTime (h, m)) =
    let (hAdd, mAdd) = x `quotRem` 60
        hNew = h + hAdd
        mNew = m + mAdd
    in if mNew >= 60
        then WallTime ((hNew + 1) `rem` 24, mNew-60)
        else WallTime (hNew, mNew)

And here is how we use it to do actual computations:

templateMethodDemo = do
    putStrLn $ "linear time: " ++ (show $ linearTimeAdd 100 (Minute 1400))
    putStrLn $ "cyclic time: " ++ (show $ cyclicTimeAdd 100 (Minute 1400))

type class minimal implementations as template method

The template method is used in frameworks, where each implements the invariant parts of a domain's architecture, leaving "placeholders" for customization options. This is an example of inversion of control. Quoted from Wikipedia

The type classes in Haskells base library apply this template approach frequently to reduce the effort for implementing type class instances and to provide a predefined structure with specific 'customization options'.

As an example let's extend the type WallTime by an associative binary operation addWallTimes to form an instance of the Monoid type class:

addWallTimes :: WallTime -> WallTime -> WallTime
addWallTimes a@(WallTime (h,m)) b =
    let aMin = h*60 + m
    in  addMinutesToWallTime aMin b

instance Semigroup WallTime where
    (<>)   = addWallTimes
instance Monoid WallTime where
    mempty = WallTime (0,0)

Even though we specified only mempty and (<>) we can now use the functions mappend :: Monoid a => a -> a -> a and mconcat :: Monoid a => [a] -> a on WallTime instances:

templateMethodDemo = do
    let a = WallTime (3,20)
    print $ mappend a a
    print $ mconcat [a,a,a,a,a,a,a,a,a]

By looking at the definition of the Monoid type class we can see how this 'magic' is made possible:

class Semigroup a => Monoid a where
    -- | Identity of 'mappend'
    mempty  :: a

    -- | An associative operation
    mappend :: a -> a -> a
    mappend = (<>)

    -- | Fold a list using the monoid.
    mconcat :: [a] -> a
    mconcat = foldr mappend mempty

For mempty only a type requirement but no definition is given. But for mappend and mconcat default implementations are provided. So the Monoid type class definition forms a template where the default implementations define the 'invariant parts' of the type class and the part specified by us form the 'customization options'.

(please note that it's generally possible to override the default implementations)

Sourcecode for this section

Creational Patterns

Abstract Factory → functions as data type values

The abstract factory pattern provides a way to encapsulate a group of individual factories that have a common theme without specifying their concrete classes. In normal usage, the client software creates a concrete implementation of the abstract factory and then uses the generic interface of the factory to create the concrete objects that are part of the theme. The client doesn't know (or care) which concrete objects it gets from each of these internal factories, since it uses only the generic interfaces of their products. This pattern separates the details of implementation of a set of objects from their general usage and relies on object composition, as object creation is implemented in methods exposed in the factory interface. Quoted from Wikipedia

There is a classic example that demonstrates the application of this pattern in the context of a typical problem in object oriented software design:

The example revolves around a small GUI framework that needs different implementations to render Buttons for different OS Platforms (called WIN and OSX in this example). A client of the GUI API should work with a uniform API that hides the specifics of the different platforms. The problem then is: how can the client be provided with a platform specific implementation without explicitely asking for a given implementation and how can we maintain a uniform API that hides the implementation specifics.

In OO languages like Java the abstract factory pattern would be the canonical answer to this problem:

• The client calls an abstract factory GUIFactory interface to create a Button by calling createButton() : Button that somehow chooses (typically by some kind of configuration) which concrete factory has to be used to create concrete Button instances.
• The concrete classes WinButton and OSXButton implement the interface Button and provide platform specific implementations of paint () : void.
• As the client uses only the interface methods createButton() and paint() it does not have to deal with any platform specific code.

The following diagram depicts the structure of interfaces and classes in this scenario:

In a functional language this kind of problem would be solved quite differently. In FP functions are first class citizens and thus it is much easier to treat function that represent platform specific actions as "normal" values that can be reached around.

So we could represent a Button type as a data type with a label (holding the text to display on the button) and an IO () action that represents the platform specific rendering:

-- | representation of a Button UI widget
data Button = Button
    { label  :: String           -- the text label of the button
    , render :: Button -> IO ()  -- a platform specific rendering action
    }

Platform specific actions to render a Button would look like follows:

-- | rendering a Button for the WIN platform (we just simulate it by printing the label)
winPaint :: Button -> IO ()
winPaint btn = putStrLn $ "winButton: " ++ label btn

-- | rendering a Button for the OSX platform
osxPaint :: Button -> IO ()
osxPaint btn = putStrLn $ "osxButton: " ++ label btn

-- | paint a button by using the Buttons render function
paint :: Button -> IO ()
paint btn@(Button _ render) = render btn

(Of course a real implementation would be quite more complex, but we don't care about the nitty gritty details here.)

With this code we can now create and use concrete Buttons like so:

ghci> button = Button "Okay" winPaint
ghci> :type button
button :: Button
ghci> paint button
winButton: Okay

We created a button with Button "Okay" winPaint. The field render of that button instance now holds the function winPaint. The function paint now applies this render function -- i.e. winPaint -- to draw the Button.

Applying this scheme it is now very simple to create buttons with different render implementations:

-- | a representation of the operating system platform
data Platform = OSX | WIN | NIX | Other

-- | determine Platform by inspecting System.Info.os string
platform :: Platform
platform =
  case os of
    "darwin"  -> OSX
    "mingw32" -> WIN
    "linux"   -> NIX
    _         -> Other

-- | create a button for os platform with label lbl
createButton :: String -> Button
createButton lbl =
  case platform of
    OSX    -> Button lbl osxPaint
    WIN    -> Button lbl winPaint
    NIX    -> Button lbl (\btn -> putStrLn $ "nixButton: "   ++ label btn)
    Other  -> Button lbl (\btn -> putStrLn $ "otherButton: " ++ label btn)

The function createButton determines the actual execution environment and accordingly creates platform specific buttons.

Now we have an API that hides all implementation specifics from the client and allows him to use only createButton and paint to work with Buttons for different OS platforms:

abstractFactoryDemo = do
    putStrLn "AbstractFactory -> functions as data type values"
    let exit = createButton "Exit"            -- using the "abstract" API to create buttons
    let ok   = createButton "OK"
    paint ok                                  -- using the "abstract" API to paint buttons
    paint exit

    paint $ Button "Apple" osxPaint           -- paint a platform specific button
    paint $ Button "Pi"                       -- paint a user-defined button
        (\btn -> putStrLn $ "raspberryButton: " ++ label btn)

Sourcecode for this section

Builder → record syntax, smart constructor

The Builder is a design pattern designed to provide a flexible solution to various object creation problems in object-oriented programming. The intent of the Builder design pattern is to separate the construction of a complex object from its representation.

Quoted from Wikipedia

The Builder patterns is frequently used to ease the construction of complex objects by providing a safe and convenient API to client code. In the following Java example we define a POJO Class BankAccount:

public class BankAccount {

    private int accountNo;
    private String name;
    private String branch;
    private double balance;
    private double interestRate;

    BankAccount(int accountNo, String name, String branch, double balance, double interestRate) {
        this.accountNo = accountNo;
        this.name = name;
        this.branch = branch;
        this.balance = balance;
        this.interestRate = interestRate;
    }

    @Override
    public String toString() {
        return "BankAccount {accountNo = " + accountNo + ", name = \"" + name
                + "\", branch = \"" + branch + "\", balance = " + balance + ", interestRate = " + interestRate + "}";
    }
}

The class provides a package private constructor that takes 5 arguments that are used to fill the instance attributes. Using constructors with so many arguments is often considered inconvenient and potentially unsafe as certain constraints on the arguments might not be maintained by client code invoking this constructor.

The typical solution is to provide a Builder class that is responsible for maintaining internal data constraints and providing a robust and convenient API. In the following example the Builder ensures that a BankAccount must have an accountNo and that non null values are provided for the String attributes:

public class BankAccountBuilder {

    private int accountNo;
    private String name;
    private String branch;
    private double balance;
    private double interestRate;

    public BankAccountBuilder(int accountNo) {
        this.accountNo = accountNo;
        this.name = "Dummy Customer";
        this.branch = "London";
        this.balance = 0;
        this.interestRate = 0;
    }

    public BankAccountBuilder withAccountNo(int accountNo) {
        this.accountNo = accountNo;
        return this;
    }

    public BankAccountBuilder withName(String name) {
        this.name = name;
        return this;
    }

    public BankAccountBuilder withBranch(String branch) {
        this.branch = branch;
        return this;
    }

    public BankAccountBuilder withBalance(double balance) {
        this.balance = balance;
        return this;
    }

    public BankAccountBuilder withInterestRate(double interestRate) {
        this.interestRate = interestRate;
        return this;
    }

    public BankAccount build() {
        return new BankAccount(this.accountNo, this.name, this.branch, this.balance, this.interestRate);
    }
}

Next comes an example of how the builder is used in client code:

public class BankAccountTest {

    public static void main(String[] args) {
        new BankAccountTest().testAccount();
    }

    public void testAccount() {
        BankAccountBuilder builder = new BankAccountBuilder(1234);
        // the builder can provide a dummy instance, that might be used for testing
        BankAccount account = builder.build();
        System.out.println(account);
        // the builder provides a fluent API to construct regular instances
        BankAccount account1 =
                 builder.withName("Marjin Mejer")
                        .withBranch("Paris")
                        .withBalance(10000)
                        .withInterestRate(2)
                        .build();

        System.out.println(account1);
    }
}

As we see the Builder can be either used to create dummy instaces that are still safe to use (e.g. for test cases) or by using the withXxx methods to populate all attributes:

BankAccount {accountNo = 1234, name = "Dummy Customer", branch = "London", balance = 0.0, interestRate = 0.0}
BankAccount {accountNo = 1234, name = "Marjin Mejer", branch = "Paris", balance = 10000.0, interestRate = 2.0}

From an API client perspective the Builder pattern can help to provide safe and convenient object construction which is not provided by the Java core language. As the Builder code is quite a redundant (e.g. having all attributes of the actual instance class) Builders are typically generated (e.g. with Lombok).

In functional languages there is usually no need for the Builder pattern as the languages already provide the necessary infrastructure.

The following example shows how the above example would be solved in Haskell:

data BankAccount = BankAccount {
    accountNo    :: Int
  , name         :: String
  , branch       :: String
  , balance      :: Double
  , interestRate :: Double
} deriving (Show)

-- a "smart constructor" that just needs a unique int to construct a BankAccount
buildAccount :: Int -> BankAccount
buildAccount i = BankAccount i "Dummy Customer" "London" 0 0

builderDemo = do
    -- construct a dummmy instance
    let account = buildAccount 1234
    print account
    -- use record syntax to create a modified clone of the dummy instance
    let account1 = account {name="Marjin Mejer", branch="Paris", balance=10000, interestRate=2}
    print account1

    -- directly using record syntax to create an instance
    let account2 = BankAccount {
          accountNo    = 5678
        , name         = "Marjin"
        , branch       = "Reikjavik"
        , balance      = 1000
        , interestRate = 2.5
        }
    print account2

-- and then in Ghci:
ghci> builderDemo
BankAccount {accountNo = 1234, name = "Dummy Customer", branch = "London", balance = 0.0, interestRate = 0.0}
BankAccount {accountNo = 1234, name = "Marjin Mejer", branch = "Paris", balance = 10000.0, interestRate = 2.0}
BankAccount {accountNo = 5678, name = "Marjin Mejer", branch = "Reikjavik", balance = 1000.0, interestRate = 2.5}

Sourcecode for this section

Functional Programming Patterns

The patterns presented in this chapter all stem from functional languages. That is, they have been first developed in functional languages like Lisp, Scheme or Haskell and have later been adopted in other languages.

Higher Order Functions

In mathematics and computer science, a higher-order function is a function that does at least one of the following:

• takes one or more functions as arguments (i.e. procedural parameters),
• returns a function as its result.

All other functions are first-order functions. In mathematics higher-order functions are also termed operators or functionals. The differential operator in calculus is a common example since it maps a function to its derivative, also a function. Quoted from Wikipedia

We have already talked about higher order functions throughout this study – in particular in the section on the Strategy Pattern. But as higher order functions are such a central pillar of the strength of functional languages I'd like to cover them in some more depths.

Higher Order Functions taking functions as arguments

Let's have a look at two typical functions that work on lists; sum is calculating the sum of all values in a list, product likewise is computing the product of all values in the list:

sum :: Num a => [a] -> a
sum []     = 0
sum (x:xs) = x + sum xs

product :: Num a => [a] -> a
product []     = 1
product (x:xs) = x * product xs

-- and then in GHCi:
ghci> sum [1..10]
55
ghci> product [1..10]
3628800

These two functions sum and product have exactly the same structure. They both apply a mathematical operation (+) or (*) on a list by handling two cases:

• providing a neutral (or unit) value in the empty list [] case and
• applying the mathematical operation and recursing into the tail of the list in the (x:xs) case.

The two functions differ only in the concrete value for the empty list [] and the concrete mathematical operation to be applied in the (x:xs) case.

In order to avoid repetetive code when writing functions that work on lists, wise functional programmers have invented fold functions:

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr fn z []     = z
foldr fn z (x:xs) = fn x y
    where y = foldr fn z xs

This higher order function takes a function fn of type (a -> b -> b), a value z for the [] case and the actual list as parameters.

• in the [] case the value z is returned
• in the (x:xs) case the function fn is applied to x and y, where y is computed by recursively applying foldr fn z on the tail of the list xs.

We can use foldr to define functions like sum and product much more terse:

sum' :: Num a => [a] -> a
sum' = foldr (+) 0

product' :: Num a => [a] -> a
product' = foldr (*) 1

foldr can also be used to define higher order functions on lists like map and filter much denser than with the naive approach of writing pattern matching equations for [] and (x:xs):

-- naive approach:
map :: (a -> b) -> [a] -> [b]
map _ []     = []
map f (x:xs) = f x : map f xs

filter :: (a -> Bool) -> [a] -> [a]
filter _ []     = []
filter p (x:xs) = if p x then x : filter p xs else filter p xs

-- wise functional programmers approach:
map' :: (a -> b) -> [a] -> [b]
map' f = foldr ((:) . f) []

filter' :: (a -> Bool) -> [a] -> [a]
filter' p = foldr (\x xs -> if p x then x : xs else xs) []

-- and then in GHCi:
ghci> map (*2) [1..10]
[2,4,6,8,10,12,14,16,18,20]
ghci> filter even [1..10]
[2,4,6,8,10]

The idea to use fold operations to provide a generic mechanism to fold lists can be extented to cover other algebraic data types as well. Let's take a binary tree as an example:

data Tree a = Leaf
            | Node a (Tree a) (Tree a)

sumTree :: Num a => Tree a -> a
sumTree Leaf = 0
sumTree (Node x l r) = x + sumTree l + sumTree r

productTree :: Num a => Tree a -> a
productTree Leaf = 1
productTree (Node x l r) = x * sumTree l * sumTree r

-- and then in GHCi:
ghci> sumTree tree
9
ghci> productTree tree
24

The higher order foldTree operation takes a function fn of type (a -> b -> b), a value z for the Leaf case and the actual Tree a as parameters:

foldTree :: (a -> b -> b) -> b -> Tree a -> b
foldTree fn z Leaf = z
foldTree fn z (Node a left right) = foldTree fn z' left where
   z'  = fn a z''
   z'' = foldTree fn z right

The sum and product functions can now elegantly be defined by making use of foldTree:

sumTree' = foldTree (+) 0

productTree' = foldTree (*) 1

As the family of fold operation is useful for many data types the GHC compiler even provides a special pragma that allows automatic provisioning of this functionality by declaring the data type as an instance of the type class Foldable:

{-# LANGUAGE DeriveFoldable #-}

data Tree a = Leaf
            | Node a (Tree a) (Tree a) deriving (Foldable)

-- and then in GHCi:
> foldr (+) 0 tree
9

Apart from several fold operations the Foldable type class also provides useful functions like maximum and minimum: Foldable documentation on hackage

In this section we have seen how higher order functions that take functions as parameters can be very useful tools to provide generic algorithmic templates that can be applied in a wide range of situations.

Origami programming style

Mathematicians love symmetry. So it comes with littly surprise that the Haskell standard library Data.List provides a dual to foldr: the higher order function unfoldr. The function foldr allows to project a list of values on a single value. unfoldr allows to create a list of values starting from an initial value:

unfoldr :: (b -> Maybe (a, b)) -> b -> [a]
unfoldr f u = case f u of
    Nothing     -> []
    Just (x, v) -> x:(unfoldr f v)

This mechanism can be used to generate finite and infinite lists:

-- a list [10..0]
ghci> print $ unfoldr (\n -> if n==0 then Nothing else Just (n, n-1)) 10
[10,9,8,7,6,5,4,3,2,1]

-- the list of all fibonacci numbers
ghci> fibs = unfoldr (\(a, b) -> Just (a, (b, a+b))) (0, 1)
ghci> print $ take 20 fibs
[0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181]

unfoldr can also be used to formulate algorithms like bubble sort in quite a dense form:

-- bubble out the minimum element of a list:
bubble :: Ord a => [a] -> Maybe (a, [a])
bubble = foldr step Nothing where
    step x Nothing = Just (x, [])
    step x (Just (y, ys))
        | x < y     = Just (x, y:ys)
        | otherwise = Just (y, x:ys)

-- compute minimum, cons it with the minimum of the remaining list and so forth
bubbleSort :: Ord a => [a] -> [a]
bubbleSort = unfoldr bubble

Unfolds produce data structures, and folds consume them. It is thus quite natural to compose these two operations. The pattern of an unfold followed by a fold (called hylomorphism is fairly common. As a simple example we define the factorial function with our new tools:

factorial = foldr (*) 1 . unfoldr (\n -> if n ==0 then Nothing else Just (n, n-1))

The unfold part generates a list of integers [1..n] and the foldr part reduces this list by computing the product [1..n].

But hylomorphisms are not limited to ivory tower examples: a typical compiler that takes some source code as input to generate an abstract syntax tree (unfolding) from which it then generates the object code of the target platform (folding) is quite a practical example of the same concept.

One interesting properties of hylomorphisms is that they may be fused – the intermediate data structure needs not actually be constructed. This technique is called deforestation and can be done automatically by a compiler.

Compressing data and uncompressing it later may be understood as a sequence of first folding and then unfolding. Algorithms that apply this pattern have been coined metamorphism.

The programming style that uses combinations of higher order functions like fold and unfold operations on algebraic data structure has been dubbed Origami Programming after the Japanese art form based on paper folds.

Higher Order Functions returning functions

Functions returning new functions are ubiqituous in functional programming as well. If we look at a simple binary arithmetic functions like (+) or (*) it would be quite natural to think that they have a type signature like follows:

(+) :: Num => (a, a) -> a

But by inspecting the signature in GHCi (with :t (+)) we see that the actual signature is

(+) :: Num a => a -> a -> a

This is because in Haskell all functions are considered curried: That is, all functions in Haskell take just one argument. The curried form is usually more convenient because it allows partial application. It allows us to create new functions by applying the original function to a subset of the formal parameters:

ghci> double = (*) 2
ghci> :t double
double :: Num a => a -> a
ghci> double 7
14

So even if we read a signature like Int -> Int -> Int informally as "takes two Ints and returns an Int", It actually should be understood as Int -> (Int -> Int) which really says "takes an Int and returns a function of type Int -> Int".

Apart from this implicit occurrence of "functions returning functions" there are also more explicit use cases of this pattern. I'll illustrate this with a simple generator for key/value mapping functions.

We start by defing a function type Lookup that can be used to define functions mapping keys to values:

-- | Lookup is a function type from a key to a Maybe value:
type Lookup key value = key -> Maybe value

-- | a lookup function that always returns Nothing
nada :: Lookup k v
nada _ = Nothing

-- | a function that knows it's abc...
abc :: Num v => Lookup String v
abc "a" = Just 1
abc "b" = Just 2
abc "c" = Just 3
abc _   = Nothing

Now we write a Lookup function generator put that adds a new key to value mapping to an existing lookup function:

-- | put returns a new Lookup function based on a key, a value and an existing lookup function:
put :: Eq k => k -> v -> Lookup k v -> Lookup k v
put k v lookup =
    \key -> if key == k
            then Just v
            else lookup key

-- and then in GHCi:
ghci> get = put "a" 1 nada

ghci> :t get
get :: Num v => Lookup String v

ghci> get "a"
Just 1

ghci> get "b"
Nothing

We can now use put to stack more key value mappings onto the get function:

ghci> get' = put "b" 2 get
ghci> get' "a"
Just 1
ghci> get' "b"
Just 2
ghci> get' "c"
Nothing

A framework for symbolic derivation of functions in calculus would be another possible application of this approach, but as it involves several more advanced features (like Template Haskell and tagged types) I won't cover it here but just point the fearless reader directly to the sourcecode: A symbolic differentiator for a subset of Haskell functions

Sourcecode for this section

Map Reduce

MapReduce is a programming model and an associated implementation for processing and generating large data sets. Users specify a map function that processes a key/value pair to generate a set of intermediate key/value pairs, and a reduce function that merges all intermediate values associated with the same intermediate key.

Our abstraction is inspired by the map and reduce primitives present in Lisp and many other functional languages. Quoted from Google Research

In this section I'm featuring one of the canonical examples for MapReduce: counting word frequencies in a large text.

Let's start with a function stringToWordCountMap that takes a string as input and creates the respective word frequency map:

-- | a key value map, mapping a word to a frequency
newtype WordCountMap = WordCountMap (Map String Int) deriving (Show)

-- | creating a word frequency map from a String.
--   To ease readability I'm using the (>>>) operator, which is just an inverted (.): f >>> g == g . f
stringToWordCountMap :: String -> WordCountMap
stringToWordCountMap =
  map toLower >>> words >>>  -- convert to lowercase and split into a list of words
  sort >>> group >>>         -- sort the words alphabetically and group all equal words to sub-lists
  map (head &&& length) >>>  -- for each of those list of grouped words: form a pair (word, frequency)
  Map.fromList >>>           -- create a Map from the list of (word, frequency) pairs
  WordCountMap               -- wrap as WordCountMap

-- and then in GHCi:
ghci> stringToWordCountMap "hello world World"
WordCountMap (fromList [("hello",1),("world",2)])

In a MapReduce scenario we would have a huge text as input that would take ages to process on a single core. So the idea is to split up the huge text into smaller chunks that can than be processed in parallel on multiple cores or even large machine clusters.

Let's assume we have split a text into two chunks. We could then use map to create a WordCountMap for both chunks:

ghci> map stringToWordCountMap ["hello world World", "out of this world"]
[WordCountMap (fromList [("hello",1),("world",2)])
,WordCountMap (fromList [("of",1),("out",1),("this",1),("world",1)])]

This was the Map part. Now to Reduce. In Order to get a comprehensive word frequency map we have to merge those individual WordCountMaps into one. The merging must form a union of all entries from all individual maps. This union must also ensure that the frequencies from the indivual maps are added up properly in the resulting map. We will use the Map.unionWith function to achieve this:

-- | merges a list of individual WordCountMap into single one.
reduceWordCountMaps :: [WordCountMap] -> WordCountMap
reduceWordCountMaps = WordCountMap . foldr (Map.unionWith (+) . coerce) empty

-- and then in GHCi:
ghci> reduceWordCountMaps it
WordCountMap (fromList [("hello",1),("of",1),("out",1),("this",1),("world",3)])

We have just performed a manual map reduce operation! We can now take these ingredients to write a generic MapReduce function:

simpleMapReduce ::
     (a -> b)   -- map function
  -> ([b] -> c) -- reduce function
  -> [a]        -- list to map over
  -> c          -- result
simpleMapReduce mapFunc reduceFunc = reduceFunc . map mapFunc

-- and then in GHCi
ghci> simpleMapReduce stringToWordCountMap reduceWordCountMaps ["hello world World", "out of this world"]
WordCountMap (fromList [("hello",1),("of",1),("out",1),("this",1),("world",3)])

What I have shown so far just demonstrates the general mechanism of chaining map and reduce functions without implying any parallel execution. Essentially we are chaining a map with a fold (i.e. reduction) function. In the Haskell base library there is a higher order function foldMap that covers exactly this pattern of chaining. Please note that foldMapdoes only a single traversal of the foldable data structure. It fuses the map and reduce phase into a single one by function composition of mappend and the mapping function f:

-- | Map each element of the structure to a monoid,
-- and combine the results.
foldMap :: (Foldable t, Monoid m) => (a -> m) -> t a -> m
foldMap f = foldr (mappend . f) mempty

This signature requires that our type WordCountMap must be a Monoid in order to allow merging of multiple WordCountMaps by using mappend.

instance Semigroup WordCountMap where
    WordCountMap a <> WordCountMap b = WordCountMap $ Map.unionWith (+) a b
instance Monoid WordCountMap where
    mempty = WordCountMap Map.empty

That's all we need to use foldMap to achieve a MapReduce:

ghci> foldMap stringToWordCountMap ["hello world World", "out of this world"]
WordCountMap (fromList [("hello",1),("of",1),("out",1),("this",1),("world",3)])

From what I have shown so far it's easy to see that the map and reduce phases of the word frequency computation are candidates for heavily parallelized processing:

• The generation of word frequency maps for the text chunks can be done in parallel. There are no shared data or other dependencies between those executions.
• The reduction of the maps can start in parallel (that is we don't have to wait to start reduction until all individual maps are computed) and the reduction itself can also be parallelized.

The calculation of word frequencies is a candidate for a parallel MapReduce because the addition operation used to accumulate the word frequencies is associatve: The order of execution doesn't affect the final result.

(Actually our data type WordCountMap is not only a Monoid (which requires an associative binary operation) but even a commutative Monoid.)

So our conclusion: if the intermediary key/value map for the data analytics task at hand forms a monoid under the reduce operation then it is a candidate for parallel MapReduce. See also An Algebra for Distributed Big Data Analytics.

Haskell provides a package parallel for defining parallel executions in a rather declarative way. Here is what a parallelized MapReduce looks like when using this package:

-- | a MapReduce using the Control.Parallel package to denote parallel execution
parMapReduce :: (a -> b) -> ([b] -> c) -> [a] -> c
parMapReduce mapFunc reduceFunc input =
    mapResult `pseq` reduceResult
    where mapResult    = parMap rseq mapFunc input
          reduceResult = reduceFunc mapResult `using` rseq

-- and then in GHCi:
ghci> parMapReduce stringToWordCountMap reduceWordCountMaps ["hello world World", "out of this world"]
WordCountMap (fromList [("hello",1),("of",1),("out",1),("this",1),("world",3)])

For more details see Real World Haskell

Sourcecode for this section

Lazy Evaluation

In programming language theory, lazy evaluation, or call-by-need is an evaluation strategy which delays the evaluation of an expression until its value is needed (non-strict evaluation) and which also avoids repeated evaluations (sharing). The sharing can reduce the running time of certain functions by an exponential factor over other non-strict evaluation strategies, such as call-by-name.

The benefits of lazy evaluation include:

• The ability to define control flow (structures) as abstractions instead of primitives.
• The ability to define potentially infinite data structures. This allows for more straightforward implementation of some algorithms.
• Performance increases by avoiding needless calculations, and avoiding error conditions when evaluating compound expressions.

Quoted from Wikipedia

Let's start with a short snippet from a Java program:

    // a non-terminating computation aka _|_ or bottom
    private static Void bottom() {
        return bottom();
    }

    // the K combinator, K x y returns x
    private static <A, B> A k(A x, B y) {
        return x;
    }

    public static void main(String[] args) {
        // part 1
        if (true) {
            System.out.println("21 is only half the truth");
        } else {
            bottom();
        }

        // part 2
        System.out.println(k (42, bottom()));
    }

What is the expected output of running main? In part 1 we expect to see the text "21 is only half the truth" on the console. The else part of the if statement will never be executed (thus avoiding the endless loop of calling bottom()) as true is always true.

But what will happen in part 2? If the Java compiler would be clever it could determine that k (x, y) will never need to evaluate y as is always returns just x. In this case we should see a 42 printed to the console.

But Java Method calls have eager evaluation semantics. So will just see a StackOverflowError...

In a non-strict (or lazy) language like Haskell this will work out much smoother:

-- | bottom, a computation which never completes successfully, aka as _|_
bottom :: a
bottom = bottom

-- | the K combinator which drop its second argument (k x y = x)
k :: a -> b -> a
k x _ = x

infinityDemo :: IO ()
infinityDemo = do
  print $ k 21 undefined -- evaluating undefined would result in a runtime error
  print $ k 42 bottom    -- evaluating botoom would result in an endless loop
  putStrLn ""

Haskell being a non-strict language the arguments of k are not evaluated when calling the function. thus in k 21 undefined and k 42 bottom the second arguments undefined and bottom are simply dropped and never evaluated.

The Haskell laziness can sometimes be tricky to deal with but it has also some huge benefits when dealing with infinite data structures.

-- | a list of *all* natural numbers
ints :: Num a => [a]
ints = from 1
  where
    from n = n : from (n + 1)

This is a recursive definition of a list holding all natural numbers. As this recursion has no termination criteria it will never terminate!

What will happen when we start to use ints in our code?

ghci> take 10 ints
[1,2,3,4,5,6,7,8,9,10]

In this case we have not been greedy and just asked for a finite subset of ints. The Haskell runtime thus does not fully evaluate ints but only as many elements as we aked for.

These kind of generator functions (also known as CAFs for Constant Applicative Forms) can be very useful to define lazy streams of infinite data.

Haskell even provides some more syntactic sugar to ease the definitions of such CAFs. So for instance our ints function could be written as:

ghci> ints = [1..]
ghci> take 10 ints
[1,2,3,4,5,6,7,8,9,10]

This feature is called arithmetic sequences and allows also to define regions and a step witdth:

ghci> [2,4..20]
[2,4,6,8,10,12,14,16,18,20]

Another useful feature in this area are list comprehensions. With list comprehensions it's quite convenient to define infinite sets with specific properties:

-- | infinite list of all odd numbers
odds :: [Int]
odds = [n | n <- [1 ..], n `mod` 2 /= 0] -- read as set builder notation: {n | n ∈ ℕ, n%2 ≠ 0}

-- | infinite list of all integer pythagorean triples with a² + b² = c²
pythagoreanTriples :: [(Int, Int, Int)]
pythagoreanTriples =  [ (a, b, c)
  | c <- [1 ..]
  , b <- [1 .. c - 1]
  , a <- [1 .. b - 1]
  , a ^ 2 + b ^ 2 == c ^ 2
  ]

-- | infinite list of all prime numbers
primes :: [Integer]
primes = 2 : [i | i <- [3,5..],  
              and [rem i p > 0 | p <- takeWhile (\p -> p^2 <= i) primes]]

-- and the in GHCi:
ghci> take 10 odds
[1,3,5,7,9,11,13,15,17,19]
ghci> take 10 pythagoreanTriples
[(3,4,5),(6,8,10),(5,12,13),(9,12,15),(8,15,17),(12,16,20),(15,20,25),(7,24,25),(10,24,26),(20,21,29)]
ghci> take 20 primes
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71]

Another classic example in this area is the Newton-Raphson algorithm that approximates the square roots of a number n by starting from an initial value a₀ and computing the approximation a_i+1 as:

a_i+1 = (a_i + n/a_i)/2

For n >= 0 and a₀ > 0 this series converges quickly towards the square root of n (See Newton's method on Wikipedia for details).

The Haskell implementations makes full usage of lazy evaluation. The first step is to define a function next that computes a_i+1 based on n and a_i:

next :: Fractional a => a -> a -> a
next n a_i = (a_i + n/a_i)/2

Now we use next to define an infinite set of approximizations:

ghci> root_of_16 = iterate (next 16) 1
ghci> take 10 root_of_16
[1.0,8.5,5.1911764705882355,4.136664722546242,4.002257524798522,4.000000636692939,4.000000000000051,4.0,4.0,4.0]

The function iterate is a standard library function in Haskell. iterate f x returns an infinite list of repeated applications of f to x:

iterate f x == [x, f x, f (f x), ...]

It is defined as:

iterate :: (a -> a) -> a -> [a]
iterate f x =  x : iterate f (f x)

As lazy evaluation is the default in Haskell it's totally safe to define infinite structures like root_of_16 as long as we make sure that not all elements of the list are required by subsequent computations.

As root_of_16 represents a converging series of approximisations we'll have to search this list for the first element that matches our desired precision, specified by a maximum tolerance eps.

We define a function within which takes the tolerance eps and a list of approximations and looks down the list for two successive approximations a and b that differ by no more than the given tolerance eps:

within :: (Ord a, Fractional a) => a -> [a] -> a
within eps (a:b:rest) =
  if abs(a/b - 1) <= eps
    then b
    else within eps (b:rest)

The actual function root n eps can then be defined as:

root :: (Ord a, Fractional a) => a -> a -> a
root n eps = within eps (iterate (next n) 1)```

-- and then in GHCI:
ghci> root 2 0.000001
1.414213562373095

This example has been taken from The classic paper Why Functional Programming Matters. In this paper John Hughes highlights higher order functions and lazy evaluation as two outstanding contributions of functional programming. The paper features several very instructive examples for both concepts.

Sourcecode for this section

Reflection

In computer science, reflection is the ability of a computer program to examine, introspect, and modify its own structure and behavior at runtime.

Quoted from Wikipedia

Reflection is one of those programming language features that were introduced first in Lisp based environments but became popular in many mainstream programming languages as it proved to be very useful in writing generic frameworks for persistence, serialization etc.

I'll demonstrate this with simple persistence library. This library is kept as simple as possible. We just define a new type class Entity a with two actions persist and retrieve with both have a generic default implementation used for writing an entity to a file or reading it back from a file. The type class also features a function getId which returns a unique identifier for a given entity, which must be implemented by all concrete types deriving Entity.

module SimplePersistence
    ( Id
    , Entity
    , getId
    , persist
    , retrieve
    ) where

-- | Identifier for an Entity
type Id = String

-- | The Entity type class provides generic persistence to text files
class (Show a, Read a) => Entity a where

    -- | return the unique Id of the entity. This function must be implemented by type class instances.
    getId :: a -> Id

    -- | persist an entity of type a and identified by an Id to a text file
    persist :: a -> IO ()
    persist entity = do
        -- compute file path based on entity id
        let fileName = getPath (getId entity)
        -- serialize entity as JSON and write to file
        writeFile fileName (show entity)

    -- | load persistent entity of type a and identified by an Id
    retrieve :: Id -> IO a
    retrieve id = do
        -- compute file path based on entity id
        let fileName = getPath id
        -- read file content into string
        contentString <- readFile fileName
        -- parse entity from string
        return (read contentString)

-- | compute path of data file
getPath :: String -> FilePath
getPath id = ".stack-work/" ++ id ++ ".txt"

A typical usage of this library would look like follows:

import SimplePersistence (Id, Entity, getId, persist, retrieve)

data User = User {
      userId :: Id
    , name   :: String
    , email  :: String
} deriving (Show, Read)

instance Entity User where
    getId = userId

reflectionDemo = do
    let user = User "1" "Heinz Meier" "hm@meier.com"
    persist user
    user' <- retrieve "1" :: IO User
    print user'

So all a user has to do in order to use our library is:

1. let the data type derive the Show and Read type classes, which provides a poor mans serialization.
2. let the data type derive from Entity by providing an implementation for getId.
3. use persist and retrieve to write and read entities to/from file.

As we can see from the function signatures for persist and retrieve both functions have no information about the concrete type they are being used on:

persist  :: Entity a => a  -> IO ()
retrieve :: Entity a => Id -> IO a

As a consequence the generic implementation of both function in the Entity type class also have no direct access to the concrete type of the processed entities. (They simply delegate to other generic functions like read and show.)

So how can we access the concrete type of a processed entity? Imagine we'd like to store our entities into files that bear the type name as part of the file name, e.g. User.7411.txt

The answer is of course: reflection. Here is what we have to add to our library to extend persist according to our new requirements:

{-# LANGUAGE ScopedTypeVariables   #-}
import           Data.Typeable

class (Show a, Read a, Typeable a) => Entity a where

    -- | persist an entity of type a and identified by an Id to a file
    persist :: a -> IO ()
    persist entity = do
        -- compute file path based on entity type and id
        let fileName = getPath (typeOf entity) (getId entity)
        -- serialize entity as JSON and write to file
        writeFile fileName (show entity)

-- | compute path of data file, this time with the type name as part of the file name
getPath :: TypeRep -> String -> FilePath
getPath tr id = ".stack-work/" ++ show tr ++ "." ++ id ++ ".txt"

We have to add a new constrained Typeable a to our definition of Entity. This allows to use reflective code on our entity types. In our case we simply compute a type representation TypeRep by calling typeOf entity which we then use in getPath to add the type name to the file path.

The definition of retrieve is a bit more tricky as we don't yet have an entity available yet when computing the file path. So we have to apply a small trick to compute the correct type representation:

    retrieve :: Id -> IO a
    retrieve id = do
        -- compute file path based on entity type and id
        let fileName = getPath (typeOf (undefined :: a)) id
        -- read file content into string
        contentString <- readFile fileName
        -- parse entity from string
        return (read contentString)

The compiler will be able to deduce the correct type of a in the expression (undefined :: a) as the concrete return type of retrieve must be specified at the call site, as in example user' <- retrieve "1" :: IO User

Of course this was only a teaser of what is possible with generic reflective programming. The fearless reader is invited to study the source code of the aeson library for a deep dive.

Sourcecode for this section

Conclusions

Design Patterns are not limited to object oriented programming

Christopher Alexander says, "Each pattern describes a problem which occurs over and over again in our environment, and then describes the core of the solution to that problem, in such a way that you can use this solution a million times over, without ever doing it the same way twice" [AIS+77, page x]. Even though Alexander was talking about patterns in buildings and towns, what he says is true about object-oriented design patterns. Our solutions are expressed in terms of objects and interfaces instead of walls and doors, but at the core of both kinds of patterns is a solution to a problem in a context. Quoted from "Design Patterns Elements of Reusable Object-Oriented Software"

The GoF Design Patterns Elements of Reusable Object-Oriented Software was written to help software developers to think about software design problems in a different way: From just writing a minimum adhoc solution for the problem at hand to stepping back and to think about how to solve the problem in a way that improves longterm qualities like extensibilty, flexibility, maintenability, testability and comprehensibility of a software design.

The GoF and other researches in the pattern area did "pattern mining": they examined code of experienced software developers and looked for recurring structures and solutions. The patterns they distilled by this process are thus reusable abstractions for structuring object-oriented software to achieve the above mentioned goals.

So while the original design patterns are formulated with object oriented languages in mind, they still adress universal problems in software engineering: decoupling of layers, configuration, dependency management, data composition, data traversal, handling state, variation of behaviour, etc.

So it comes with little surprise that we can map many of those patterns to commonly used structures in functional programming: The domain problems remain the same, yet the concrete solutions differ:

• Some patterns are absorbed by language features:
  • Template method and strategy pattern are no brainers in any functional language with functions as first class citizens and higher order functions.
  • Dependency Injection and Configuration is solved by partial application of curried functions.
  • Adapter layers are replaced by function composition
  • Visitor pattern and Interpreters are self-evident with algebraic data types.
• Other patterns are covered by libraries like the Haskell type classes:
  • Composite is reduced to a Monoid
  • Singleton, Pipeline, NullObject can be rooted in Functor, Applicative Functor and Monad
  • Visitor and Iterator are covered by Foldable and Traversable.
• Yet another category of patterns is covered by specific language features like Lazy Evaluation, Parallelism. These features may be specific to certain languages.
  • Laziness allows to work with non-terminating compuations and data structures of infinite size.
  • Parallelism allows to scale the execution of a program transparently across CPU cores.

Design patterns reflect mathematical structures

What really struck me in the course of writing this study was that so many of the Typeclassopedia type classes could be related to Design Patterns.

Most of these type classes stem from abstract algebra and category theory in particular. Take for instance the Monoid type class which is a 1:1 representation of the monoid of abstract algebra. Identifying the composite pattern as an application of a monoidal data structure was an eye opener for me:

Design patterns reflect abstract algebraic structures.

As another example take the Map-Reduce pattern: we demonstrated that the question whether a problem can be solved by a map-reduce approach boils down to the algebraic question whether the data structure used to hold the intermediary results of the map operation forms a monoid under the reduce operation.

Rooting design patterns in abstract algebra brings a higher level of confidence to software design as we can move from 'hand waving' – painting UML diagrams, writing prose, building prototypes, etc. – to mathematical reasoning.

Mark Seemann has written an instructive series of articles on the coincidence of design patterns with abstract algebra: From Design Patterns to Category Theory.

Jeremy Gibbons has also written several excellent papers on this subject:

Design patterns are reusable abstractions in object-oriented software. However, using current mainstream programming languages, these elements can only be expressed extra-linguistically: as prose,pictures, and prototypes. We believe that this is not inherent in the patterns themselves, but evidence of a lack of expressivity in the languages of today. We expect that, in the languages of the future, the code parts of design patterns will be expressible as reusable library components. Indeed, we claim that the languages of tomorrow will suffice; the future is not far away. All that is needed, in addition to commonly-available features, are higher-order and datatype-generic constructs; these features are already or nearly available now.
Quoted from Design Patterns as Higher-Order Datatype-Generic Programs

He also maintains a blog dedicated to patterns in functional programming.

I'd like to conclude this section with a quote from Martin Menestrets FP blog:

[...] there is this curious thing called Curry–Howard correspondence which is a direct analogy between mathematical concepts and computational calculus [...].

This correspondence means that a lot of useful stuff discovered and proven for decades in Math can then be transposed to programming, opening a way for a lot of extremely robust constructs for free.

In OOP, Design patterns are used a lot and could be defined as idiomatic ways to solve a given problems, in specific contexts but their existences won’t save you from having to apply and write them again and again each time you encounter the problems they solve.

Functional programming constructs, some directly coming from category theory (mathematics), solve directly what you would have tried to solve with design patterns.

Quoted from Geekocephale

some interesting links

IBM Developerworks

Design patterns in Haskell

GOF patterns in Scala

Patterns in dynamic functional languages

Scala Typeclassopedia

FP resources