-
Notifications
You must be signed in to change notification settings - Fork 11
/
ekganalysis.py
115 lines (87 loc) · 3.12 KB
/
ekganalysis.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
# -*- coding: utf-8 -*-
"""ekgAnalysis.ipynb
Automatically generated by Colaboratory.
Original file is located at
https://colab.research.google.com/drive/1ge58XuA5vdBTjgBPc1NoXQPvZ0JG_jG5
"""
from matplotlib import pyplot as plt
import matplotlib
import pandas
import numpy as np
from scipy.fftpack import fft
ekgDF = pandas.read_csv('ekg.csv')
print ('Sampling frequency is: ')
samplingFreq = 1/(ekgDF['Time (s)'][22]-ekgDF['Time (s)'][21])
print (samplingFreq)
ekgDF
# Time Domain Signal
matplotlib.rc('figure', figsize=(15, 8))
plt.plot(ekgDF['Time (s)'],ekgDF['Channel 1 (V)'])
# Frequency Domain
# FFT len is half size of the signal len
# Because of nyquist theorem only half of the sampling frequency can be seen in the sprectrum
ekgData = ekgDF['Channel 1 (V)'].values
fftData = np.abs( fft(ekgData) )
fftLen = int(len(fftData) / 2)
freqs = np.linspace(0,samplingFreq/2, fftLen )
matplotlib.rc('figure', figsize=(20, 8))
plt.figure()
plt.plot( freqs, fftData[0:fftLen] )
plt.figure()
plt.plot( freqs[0:400], fftData[0:400] )
## Design IIR filter
from scipy import signal
sos = signal.iirfilter(17, [49, 51], rs=60, btype='bandstop',
analog=False, ftype='cheby2', fs=4000,
output='sos')
w, h = signal.sosfreqz(sos, 2000, fs=2000)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.semilogx(w, 20 * np.log10(np.maximum(abs(h), 1e-5)))
ax.set_title('Chebyshev Type II bandpass frequency response')
ax.set_xlabel('Frequency [Hz]')
ax.set_ylabel('Amplitude [dB]')
ax.axis((10, 1000, -100, 10))
ax.grid(which='both', axis='both')
plt.show()
## filter out 50 Hz noise
ekgFiltered = signal.sosfilt(sos, ekgData)
# Time Domain Signal
matplotlib.rc('figure', figsize=(15, 8))
plt.plot(ekgDF['Time (s)'],ekgFiltered)
# Frequency Domain
# FFT len is half size of the signal len
# Because of nyquist theorem only half of the sampling frequency can be seen in the sprectrum
fftData = np.abs( fft(ekgFiltered) )
fftLen = int(len(fftData) / 2)
freqs = np.linspace(0,samplingFreq/2, fftLen )
matplotlib.rc('figure', figsize=(15, 8))
plt.figure()
plt.plot( freqs, fftData[0:fftLen] )
plt.figure()
plt.plot( freqs[0:400], fftData[0:400] )
## Design IIR filter
sos2 = signal.iirfilter(17, [0.5, 200], rs=60, btype='bandpass',
analog=False, ftype='cheby2', fs=4000,
output='sos')
w, h = signal.sosfreqz(sos2, 2000, fs=2000)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.semilogx(w, 20 * np.log10(np.maximum(abs(h), 1e-5)))
ax.set_title('Chebyshev Type II bandpass frequency response')
ax.set_xlabel('Frequency [Hz]')
ax.set_ylabel('Amplitude [dB]')
ax.axis((10, 1000, -100, 10))
ax.grid(which='both', axis='both')
plt.show()
## filter out 50 Hz noise
ekgFiltered2 = signal.sosfilt(sos2, ekgFiltered)
# Time Domain Signal
matplotlib.rc('figure', figsize=(15, 8))
plt.plot(ekgDF['Time (s)'],ekgFiltered2)
"""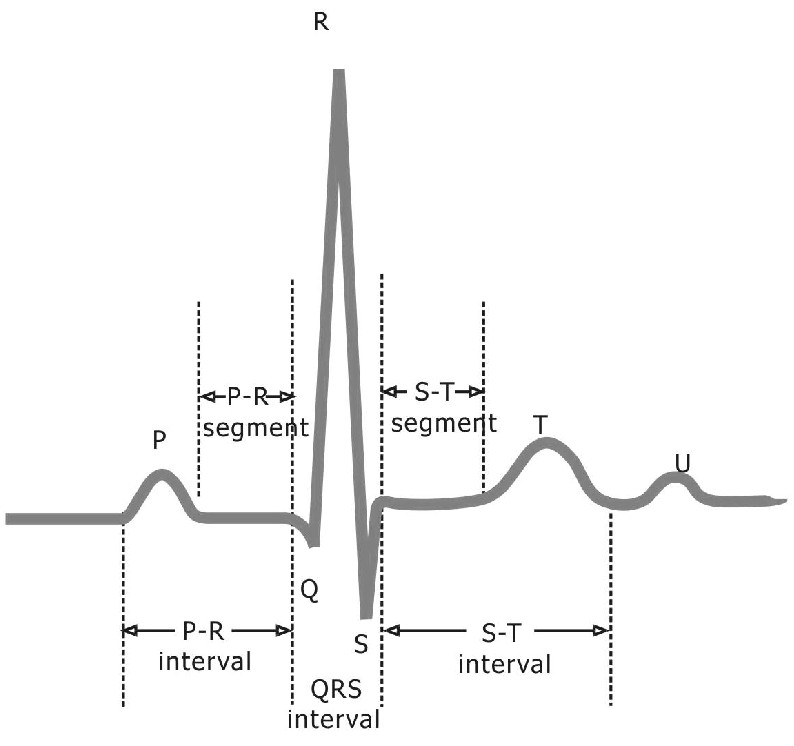"""
def moving_average(x, w):
return np.convolve(x, np.ones(w), 'same') / w
# Time Domain Signal
matplotlib.rc('figure', figsize=(15, 8))
plt.plot(ekgDF['Time (s)'],moving_average(ekgFiltered2, 100))