Introduction | Install | Default Usage | Adjusting # of Significant Figures on Error | Adjusting cutoffs for switch to scientific notation | Render Latex in Jupyter | Get Rounded Numbers Instead of Strings | Comments and Bug Reporting | Change Log | License

Round Using Error

Introduction

This package provides opinionated tools for formatting the output of values with known errors. The general format is value +/- error. The values are rounded so that the last digit reported for the value is the same order of magnitude as the least significant digit reported on the error. The default is to report the error to two significant figures. The opinionated part is that the output switches automatically from decimal to scientific notation. Scientific notation is used for values < 0.1 and > 1000. Where the switch occurs can be changed with optional parameters.

The output is available as:

• tuple of strings (value, error, power_of_ten);
• text in format value +/- error;
• latex in the form value \pm error.
• rounded floating point numbers (value, error)

Usage

Install using pip

pip install -U round_using_error.

Default usage:

>>> from round_using_error import *
>>> rndwitherr(0.001234, 0.000241)
('1.23', '0.24', '-3')
>>> rndwitherr(1299.845, 0.124)
('1.29985', '0.00012', '3')
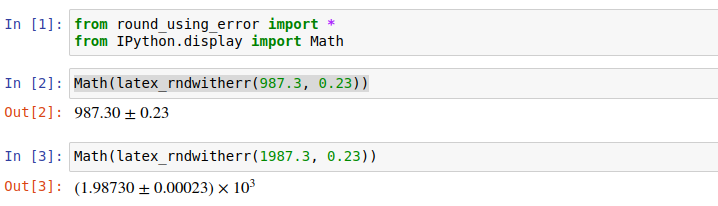
>>> text_rndwitherr(1299.845, 0.124)
'(1.29985 +/- 0.00012) X 10^3'
>>> latex_rndwitherr(1299.845, 0.124)
'(1.29985\\pm0.00012)\\times 10^{3}'
>>> rndwitherr(0.001234, 0.000241)
('1.23', '0.24', '-3')
>>> text_rndwitherr(0.001234, 0.000241)
'(1.23 +/- 0.24) X 10^-3'
>>> latex_rndwitherr(0.001234, 0.000241)
'(1.23\\pm0.24)\\times 10^{-3}'
>>> rndwitherr(0.1234, 0.024)
('0.123', '0.024', '')
>>> text_rndwitherr(0.1234, 0.024)
'0.123 +/- 0.024'
>>> latex_rndwitherr(0.1234, 0.024)
'0.123\\pm0.024'

Adjusting significant figures on error

>>> from round_using_error import *
>>> latex_rndwitherr(0.1234, 0.024)
'0.123\\pm0.024'
>>> rndwitherr(0.001234, 0.000241, errdig = 1)
('1.2', '0.2', '-3')
>>> rndwitherr(0.001234, 0.000241, errdig = 3)
('1.234', '0.241', '-3')
>>> text_rndwitherr(0.001234, 0.000241, errdig = 3)
'(1.234 +/- 0.241) X 10^-3'
>>> latex_rndwitherr(0.001234, 0.000241, errdig = 3)
'(1.234\\pm0.241)\\times 10^{-3}'

Adjusting the cutoffs for switching to scientific notation

>>> rndwitherr(1247.325, 1.23, errdig = 1, highmag = 3)
('1247', '1', '')
>>> rndwitherr(3.53e-2,2.24e-3, errdig = 1, lowmag = -2)
('0.035', '0.002', '')

Render Latex in Jupyter

Get Rounded Numbers for the Value and Error

It is possible to get floating point numbers rounded as done by this package rather than string representations, using the function numbers_rndwitherr(). However, because of the way floating point numbers are printed, they may not display with proper significant figures (see below). Use the functions described above that return strings to guarantee proper significant figures.

>>> numbers_rndwitherr(0.002345,0.0072)
(0.002, 0.007)
>>> numbers_rndwitherr(2.345864,0.0072)
(2.3459, 0.0072)
>>> numbers_rndwitherr(2.345864e-3,0.0072e-2)
(0.002346, 7.2e-05)
>>> numbers_rndwitherr(83e-4, 0)
(0.0083, 0)

Specifying number of error digits

>>> numbers_rndwitherr(1247.325, 1.23, errdig = 3)
(1247.33, 1.23)

Default floating point display may not give proper significant figures.

Compare the output of numbers_rndwitherr and rndwitherr.

>>> numbers_rndwitherr(1247.325, 1.23, errdig = 1) # bad
(1247.0, 1.0)
>>> rndwitherr(1247.325, 1.23, errdig = 1, highmag = 3) # good
('1247', '1', '')

Issues or Comments

Ideas, suggestions, bug reports and general comments are welcome . Please use the github repository issues tracker: https://github.com/gutow/round_using_error/issues.

Change Log

• 1.2.0 Introduced numbers_rndwitherr() function. Readme.md and docs updates.
• 1.1.1 More doctests. Tweaked handling of errors larger than values.
• 1.1.0 Increased error checking. Now raises warning for negative error values. Also fixes an error that occurred with negative values.

This software is distributed under the GNU V3 license

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

Copyright - Jonathan Gutow, 2021, 2022.