• Digitális tankönyvtár: A gépi látás és képfeldolgozás párhuzamos modelljei és algoritmusai
• Kató Zoltán - Digitális képfeldolgozás
  • Digitális képfeldolgozás gyakorlat
• R.C. Gonzales, R.E. Woods: Digital Image Processing
• Rövid András; Sergyán Szabolcs; Vámossy Szabolcs - A gépi látás és képfeldolgozás párhuzamos modelljei és algoritmusai

Számítógépes képfeldolgozás

• képfeldolgozás: https://users.nik.uni-obuda.hu/vamossy/Kepfeldolgozas2019/
• gépi látás: https://users.nik.uni-obuda.hu/vamossy/GepiLatas2019/

követlemény:

• 1 beadandó bejelenető március elejéig
• 2 beadandó
  • kis photoshop: fontos az algoritmusok gyorsítása!
    • Negálás *
    • Gamma transzformáció
    • Logaritmikus transzformáció
    • Szürkítés *
    • Hisztogram készítés
    • Hisztogram kiegyenlítés
    • Átlagoló szűrő (Box szűrő)
    • Gauss szűrő
    • Sobel éldetektor
    • Laplace éldetektor
    • Jellemzőpontok detektálása
  • saját téma, pl: kép elemzés, biometrikus adat elemzés, műholdkép elemzés, MR, stb
• 1 zh a félév végén

EA 1

• Richard Szeliski könyve!

technika fejődése:

• orvoslás, ICT fejlődése
• kémműholdak
• katonai fejlesztések

mi a digitálsi tér fogalma:

• kétdimenziós függvény ahol az x és y koodináták f amplitódújú az (x,y) koordinátákban a intenzitás vagy a szürkeségi szint
• ha x,y,f diszkrét mennyiségek akor a képet digitálsinak mondjuk

Mi a képfeldolgozás?

• Szegmentálás (részekre bontás), leírók kinyerése
• Osztályozás, analízálás, megértés

Digitális képfeldolgozás (Digital image processing, DIP): digitális képek feldolgozása digitális számítógépekkel; képek fokozása, vagy más manipulálása, az eredmény általában másik kép (és valamilyen jellemzők)

Számítógépes látás, vagy röviden gépi látás (Computer Vision, CV): számítógép használata az emberi látás emulációjára, amely magába foglalja a tanulást, a következtetést és a reagálást (leírás, analízis, megértés). A mesterséges intelligencia (Artificial Intelligence, AI) több részét használják a CV-ben, mint a DIP-ben

Zaj kezelése

ismétlődő zaj

mivel a képfeldolgozás sokszor az ilyen átsázmítást használja fel különböző jellemzők elemzésére

• durva válltozás
• hirtelen változás a kontúrok mentén
• adott közte tartományt próbál hatékonyan kezelni

javasolt nagyobb terjedelmű nyers formákat használni, szemben a nagyobb tömörítést használó képekkel, mert a tömörített kép visszafejtése szinte sosem teljes, valmaint tömörítés után már kis anomáliák is megjelenhetnek

A digitális képfeldolgozás szintjei

• Alacsony szint: mind az input mind az output kép
• Közép szint: képek részekre bontása valamiylen jellemző alapján, pl hasonló sínek, fomrák, stb
• Magas szint: a felismert objektumok együttesének érzékelése, mesterséges inteligencia használatával, osztályokat határozunk meg, analizálunk jeleneteket

részekre bontás:

Mi a gépi látás (Computer Vision)?

térbeli modellek visszaállíása képekből, képsorozatokból

• milyen kamerákat használunk, vagy akmerák vagy szenzorok
• pl motion capture: felvesszük a mozását egy objektumnak, és rávetítjük egy 3d avatarra.

Miért bonyolult a számítógépes látás?

Jelenetek megértése, még komplex és rendezetlen kép esetében is egyszerű az ember számára, a gép számára viszont a külön egységek azok amiket lát, ért, a tlejes egész az amit nem.

szín szerepe: A színek intenzitását figylehetjük, de fontos, hogy milyen színmodellt használunk ekkor, mert a használt fényintenzitás változtathat a színeken, és csalóka lehet.

textúra: a textúrák használata is jó lehet de bizonyos ismétlődést nem tud kizárni.

alak szerepe: a formák észlelése is érdekes lehet, de kérdés, hogy például az árnyék és hasonló dolgok emnnyire befolyásolják az alak értlemezését

Vegyük figyelembe a jelenet körülményeit

• Gyűjtsünk minél több adatot (képet)
• Vegyük figyelembe a környező világ jellemzőit
• Számíthatóság és robosztusság

A számítógépes látórendszereknél, általában az iparban:

• A megvilágítási feltételeket mi szabályozzuk
• Az objektumot mi pozícionáljuk
• Az objektum jellemzőiben rejlő lehetőségeket használjuk ki

mélytanuláshoz:

1. rengeteg reprezentatív adat kell
2. amit lehet tegyünk meg az adatok befolyásolására, pl megvilágítás, háttér, stb

Gépi látás eléri-e, megelőzi-e az emberi látást?

https://regi.tankonyvtar.hu/hu/tartalom/tamop412A/2011-0063_15_gepi_latas/ch02s03.html

• emberek “összetett” dolgokban jobbak
• számítógép „egyszerű” dolgokban jobb

a gépi látás képes megoldani:

• Föld megjelenítők (3D modell)
• Photo Tourism technology
• Optikai karakterfelismerés (OCR): dokumentumok szkennelése, szöveggé alakítása, rendszám felismerés
• ujjlenyomat, arcfelismerő rendszer
• Objektum felismerés (mobil telefonokban)
• Speciális effektusok
  • motion capture technika
• sport
• Okos autók
• Űralkalmazás
• 3D terepmodellezés
• Akadály detektálás, helyzet követés
• Autonóm robotnavigáció (Autonomous robot navigation)
• Számítógépes felügyelet és összeszerelés (Inspection and assembly)
• 3D képalkotás - MRI, CT
• Képvezérelt sebészet

https://computervisiononline.com/

The Computer Vision Industry ~ David Lowe

Adatstruktúrák a képfeldolgozásban

A képet alpvetően egy kétdimenziós tömbként tudjuk elképzelni, de a memóriában valójában ez egyetlen hosszú karaktersorozat. Amennyiben ez egy színes kép úgy ez egy 3 dimenziós érték R G B értékkel.

Ahhoz, hogy a képpontokat azonosítnai tudjuk szükségünk van koordináta rendszerre, mivel és milyen irányba mérünk értékeket? Egy ilyen pont a pixel, ami egy kis tégalalp, ami vagy szürgeésgi vagy színcsatorna szerinti intenzitás értéket jelent.

Számítási ígény:

• Tételezzünk fel egy 1024 × 1024 pixelből álló képet, ahol az intenzitást 8-biten tároljuk.
• Tárolási igény 2^20 byte (1 Mbytes)
• Tegyük fel, hogy minden pixelen csak egy műveletet végzünk, ekkor 2^20 operációt kell végeznünk a képen. Ez kb. 10^-8 mp/művelet, ami hozzávetőlegesen 10 ms-ot igényel.
• Valós idejű képfeldolgozás esetén tipikusan 25-30 képet kell másodpercenként feldolgozni (fps).
• Tipikusan nem csak egyetlen műveletet kell pixelenként elvégezni, hanem több és összetettebb funkciókat.

Hisztogram

Azt adja meg, hogy az egyes intenzitásokból hány darab van a képen, azaz egy gyakoriságot ad meg.

for(i = 0; i < height_max; x++)
    for(j = 0; j < width_max; y++)
        hist[p[i][j]] = hist[p[i][j]] + 1;
/*A pixeleket a p[][] tömb tárolja és a hist[k] vektor megmondja, hogy a k-ik intenzitásból hány darab van a képen*/        

végighaladunk a képen minden egyes sorban megnézzük, hogy az adott intenzitás amit éppen kiolvasunk milyen értéket reprezentál és a hisztogramban az adott értken növeljük az elővordulások számát. Teháét ez egy egyszerű összegzés, könnyen párhuzamosítható.

normalizálás: elosztjuk az egyes képpontok gyakoriságát a képpontok számával.

Halmozott hisztogram: egy bizonyos intenzitásig hány darab annál nem nagyobb intenzitási érték jelenik meg a képen. A halmozás mindne szóbajövő intenzitásra elvégezhető. a nullás halmozás megegyezik a nullás hisztogram értékkel

Integrál kép

Összegzés, egy téglalap alakú részben adja meg az intenziátások összegét. Előnye, hogy gyorsan számolható.

Minden x és y koordinátára összedjuk és megkapjuk a halmozott képet.

Legyen i a képpont intenzitása, ii az integrált kép

• s adott pozícióban oszlopösszeg amit korábbi számításból tudunk: S(x , y) = s (x , y - 1) + i (x , y)
• ii (x , y) = ii (x - 1, y) + s (x , y) és s (x,- 1) = 0, ii (- 1, y) = 0

D téglalap számítása: ii(4) – ii(3) – ii(2) + ii(1)

Ezt az arc detektáláshoz érdemes használnni, neve Haar-szerű jellemzők: Haar-szerű jellemzők: (Képpont intenzitások összege a fekete területen) - (Képpont intenzitások összege a fehér területen)

Hogyan? A maszkokat végigfuttatjuk a képen, és számoljuk a jellemzőket:

Műveletígények:

• Téglalap számítása: négy tömbhivatkozás
• Két téglalap: hat tömbhivatkozás
• Három téglalap: 8 tömbhivatkozás
• Négy téglalap: 9 tömbhivatkozás

EA 2

Előfeldolgozási lépések, van egy bemeneti képünk és abból szeretnénk valamilyen szmepontból jobb képet. Ez történhet képtérben, pontműveletekkel, ha a koordinátán kiolvassuk azi ntnezitást, megváltoztatjuk és ugyanoda visszaírjuk. Halmozott relatív gyakoriságokat sázmolunk egy adott határig, és az alapján módosítjuk a képet.

hisztogram kiegynelítés

http://www.inf.u-szeged.hu/~tanacs/pyocv/hisztogram_kiegyenlts.html

• minden egyes képnek elkészítjük a hisztogramját
• kiszámoljuk minden pixelre a relatív értéket, majd

átlagolás

képminőség javítása több kép átalgával

sok zajos kép esetén a zaj átlaga nulla

kivonás

változást lehet detektálni

• készítünk egy háttérmodellt pl utcakép
• megjön a változás, kivontjuk a kettőt egymásból, megkapjuk a változást magát pl jármű

and/or képre alkalmazva

a számunkra érdekes részt lehet kiemelni, ha az alp képre egy fehér alapon fekete vagy fekete alapon fehér kijelölést jelző képel összeéseljük vagy vagyokljuk

képek transzformálása/inverz transzformálása

forgatás/eltolás esetén az eredeti képből az elforgatás után készült képen lehetnek lyukak amikhez nem tartozik eredeti képpont ekkor inverz transzformációval visszaszámolhatjuk a szomszédos képpontokat kiemelve behelyettesíhetjük.

Invert Filter

forrás: https://www.codeproject.com/Articles/1989/Image-Processing-for-Dummies-with-C-and-GDI-Part-1

public static bool Invert(Bitmap b)
{
    // GDI+ still lies to us - the return format is BGR, NOT RGB. 
    BitmapData bmData = b.LockBits(new Rectangle(0, 0, b.Width, b.Height), 
        ImageLockMode.ReadWrite, PixelFormat.Format24bppRgb);  //a BitMap nem rgb hanem bgr sorrendben tároljaa színeket!
    int stride = bmData.Stride;  //képsor futam, azt adja a meg, hogy a memóriában a kép milyen széles legyen, ugynaakkor ez nem feltétlen egyenlő a teljes képszélességgel, csak ha az pontosan osztható vele
    System.IntPtr Scan0 = bmData.Scan0; //egy olyan pointer ami rámutat a memóriterület kezdetére ahol a bitmapp kezdődik
    unsafe 
    { 
        byte * p = (byte *)(void *)Scan0;
        int nOffset = stride - b.Width*3; 
        int nWidth = b.Width * 3;     //
        for(int y=0;y < b.Height;++y) //soronként fledolgozzuk a képet
        {
            for(int x=0; x < nWidth; ++x )  //byteonként feldolgozzuk a sort //lehetne e helyett a teljes sort negálni is
            {
                p[0] = (byte)(255-p[0]);  //negálja a pixelt
                ++p;
            }
            p += nOffset; //sort ugrunk
        }
    }

    b.UnlockBits(bmData);

    return true;
}

Grayscale filter

unsafe
{
    byte * p = (byte *)(void *)Scan0;

    int nOffset = stride - b.Width*3;

    byte red, green, blue;

    for(int y=0;y < b.Height;++y)
    {
        for(int x=0; x < b.Width; ++x )
        {
            blue = p[0];
            green = p[1];
            red = p[2];

            p[0] = p[1] = p[2] = (byte)(.299 * red 
                + .587 * green 
                + .114 * blue); //gyorsabb volna ha egésszé alakítanánk vagy lookup tablet használnánk

            p += 3;
        }
        p += nOffset;
    }
}

Brightness filter

for(int y=0;y<b.Height;++y)
{
    for (int x = 0;  x < nWidth; ++x)
    {
        nVal = (int) (p[0] + nBrightness);

        if (nVal < 0) nVal = 0;
        if (nVal > 255) nVal = 255;

        p[0] = (byte)nVal;

        ++p;
    }
    p += nOffset;
}

szűrés képtéren

Maszk használata

• adott input minden pixelére maszkot helyezünk, úgy, hogy annak origója az adott pixelekre essék
• az input maszk alatti pixleeit megszorozzuk a maszkban szereplő súlyokkkal
• az eredmény: az input helyzetének megfelelő pixel

lineáris szűrés

megszorzunk súly intenzitásokat és úgy akpunk kép értékeket

az ouput lineáris

• simító: átlagoló
• élesítő
  • alul/felül áteresztő szűrők
  • sávszűrők
  • derivált szűrők

nem lineáris szűrés

• medián szűrő
• simítás

EA 3

Bionoiális eloszlás

Gauss szűrő: 1/16*[[1 2 1][2 4 2][1 2 1]]. A binomiális eloszlás is közelít a normális eolszláshoz, tehát közleít a Gauss szűrő értékeéhez.

Nem lineáris szűrők, medián szűrő

sorbarendező szűrő, a medián eltűnteti a pixeles zajokat.

Egy környezetből (3x3,5x5), kiolvassuk az értékeket,

példa kód:

1. allocate outputPixelValue[image width][image height]
2. allocate window[window width × window height]
3. edgex := (window width / 2) rounded down
4. edgey := (window height / 2) rounded down
   for x from edgex to image width - edgex do
   for y from edgey to image height - edgey do
       i = 0
       for fx from 0 to window width do
           for fy from 0 to window height do
               window[i] := inputPixelValue[x + fx - edgex][y + fy - edgey]
               i := i + 1
       sort entries in window[]
       outputPixelValue[x][y] := window[window width * window height / 2]

Párhuzmaosíthatunk, ha mindig a vertikális és a horizontálsi irányban összehasonlítjuk és felcseréljük egymás között a műveleteket.

A sarkokat a (3x3)-as levágja! a 9x9-es nem!

• impulus szerű zajokat eltávolíŧ
• nem szélesíti ki az éleket
• nem mindig hatékony

Élesítés

A maszklunkban negatív és pozitív érétkek is lesznek, mivel az a cél, hogy a homogén területen 0 érétket kapjunk máshól attól eltérőt, így növeljük a kontraszt értéket.

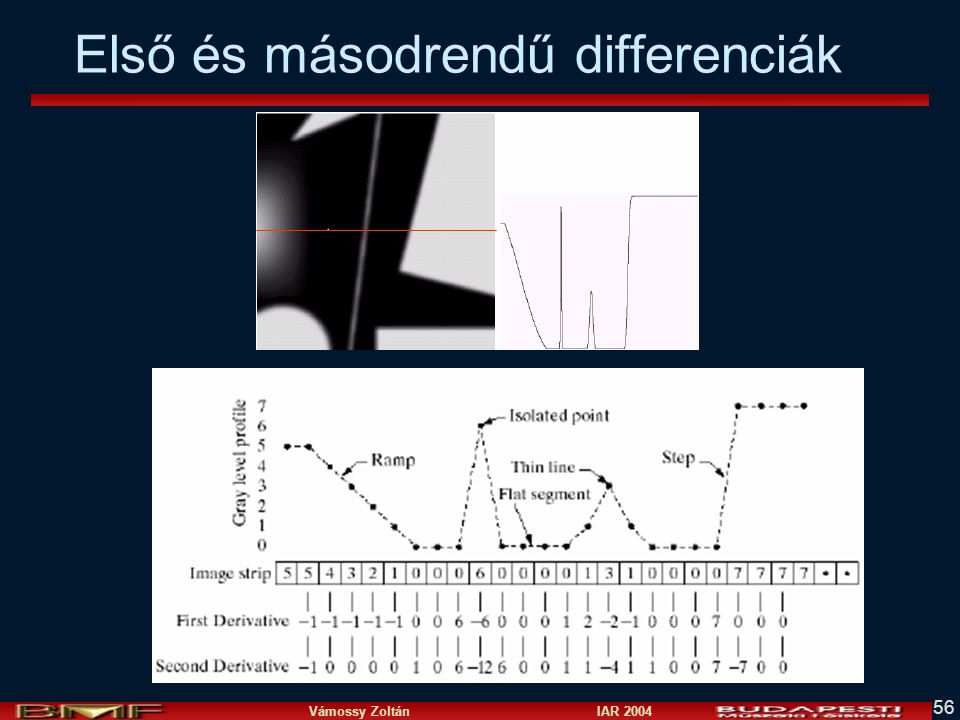
Ehhez gradienst használunk:

A gyakorlatban ez azt jelenti, hogy első deriváltat úgy kapjuk, hogy a kelsorozatból két érték különbségét vesszük, másod deriváltnak a kapott különbésgeket számoljuk tovább újabb különbséget kapva.

A fenti példából kiindulva a konstans szakszon az előtte kapott differneciákat kapjuk. Így lesz a 3. helyen -1 miután 5-6 = -1. Tehát a derivált után, ez azt jelenti, hogy a minden változás kicsit normalizáltabb lesz, és a második derivált értéke ha pozitív értékből negatívba (vagy fordítva) ment akkor nagy változás volt a képen.

élesítéshez térbeli deriváltakat használunk -> gradiens két irányból ->másodrendű differenciáltak

• számoljuk ki x és rá merőleges y irányban a derivált értékét
• a két értékből sázmítsunk vektor eredőt, és annak az irányát és nagyságát is határozzuk meg.

Laplace szűrő

x irányú derivált és y irányú drivált összege

A lehetséges maszkjaink:

0  1  0    1  1  1
1 -4  1    1 -8  1
0  1  0    1  1  1 

0 -1  0   -1 -1 -1
-1 4 -1   -1  8 -1
0 -1  0   -1 -1 -1

Ez 4 különböző maszk, az első és az laatta levő ugynaolyan, a bal felső és alatta levő a küönböző irányokat is figyelembe veszi.

tehát: diff2(f)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4*f(x,y)

Él detektálás

Alapflevetés: hol van nagy változás a képen. Ez objektumok határait/vaonalait jól leírja.

• ha éleket akarunk detektálni előbb használjunk zajszűrést
• élkiemelés
• éldetektálás
• éllokalizálás

euklédeszi távolság: négyzetek összegének gyöke

manhattan távolság: abszolút értékben a két irány nagyságának összege

Prewitt operátor

• átlagolás egyik irányban
• a maszk elemek összértéke nulla
• kevésbé zaj érzékeny felbontható két külön mezőre, egy függőleges és egy vízszintes irányban, ekkor külön-külön elvégezhetjük a vízszintes és függőleges detektálást és ekkor megkapjuk a végeredményt ha összetesszük a két külön képet.

Canny éldetektor

• élkiemelés
• nem maximumok elnyomása
• histerézises küszöbölés
• gauss zajos képeken
• lépcsős képeken használható

ideális éldetektálás:

1. gauss szűréssel simitás
2. kétirányú gradiens számítás
3. normális és erősség számítás
4. kiszámolja az élnormális irányát és elvékonyítja ott a képet
5. összeköttjük az élpontokat láncolt listákban
6. hysteresises küszöbölés

EA 4 - Élek, sarokpontok, speciális szakaszok

1. zajszűrés
2. deriváltakhoz tartozó operátorokkal dolgozunk, vagy differenciáló oerátorokat. Két irányú operátort használunk, egy a vízszintes, egy a függőleges irányban, ez a gradiensvektor.

Éldetektor

Éldetektornál elég egy 3x3-as operátor, ilyen Prewitt operátor is, egyik iránban simít másik irányban "detektál"

-1 -1 -1    -1  0  1
 0  0  0    -1  0  1
 1  1  1    -1  0  1

Kis méretű maszkok esetében nem javasolt a kettős ciklus használata amin belül egy maszkoló függvényt használjunk, inkább, elég a pixel érétkeket megfelelő előjellel összegezni, sőt, a gradinest is számolhatjuk: grad(f) = |(x2-x0)+(x5-x3)+(x8-x6)|+|(x6-x0)+(x7-x1)+(x8-x2)|.

LOG operátor

A változásokat értékeljük ki, hogy hol van ellentétes irányú átmenet.

DOG operátor

A bnormális eloszlások különbségét veszi figylemebe, tehát a gaussok differenciáljának különbséégét nézi.

Minta összehaasonlítása képrészlettel

Fogoma mintát és ráillesztem a képrészletre, amennyiben az egmyásnak megfeleltethető pozícióban levő pixelek értékeit kivonuk egymásból úgy megkapjuk ak öztük levő különbséget. Ha fogjuk a minta és a kép intenzitásának különbségének abszolút értékét és képezzük minden képpontra akkor vesszük azok minimumát.

Jellemző pont detektálás

Kép illesztés/párosítás szempontjából ki lehet választani, valamilyen szmepontból jellemző pontjait a képnek. Ez jó lehet pl ugyanarról a dologról készült képek összeillesztéséhez. Olyan pontokat veszünk figyelembe, amik geometriai transzformációkra invariánsak, így szeretnénk olyan jellemzőpontokat amikkel. A jellemzőpont mellé valamilyen tulajdonságot is illeszthetünk, ekkor jellemző detektorokat készítünk.

Irodalom: Brown: Multi-Image Matching using Multi-Scale Oriented Patches

• fontos, hogy gyorsan sázmíthatóak legyenek
• elég pontos válaszokat adjanak
• ne legyen túl sok
• a térbeli elhelyezkedést tudjuk figyelembe venni

Definiálunk egy ablakot amit "tologatunk" a képen, ha nincs semmi akkor az egy homogén terület, ha egy élen vagyunk és az él mentén mozgunk akkor ugyanolyan az eredeti éa az elmozdított akkor nincs eltérés, ellenben ha ellentétes irányban mozgatjuk akkor lesz változás, ha sarok fölött játszuk ezt el akkor minden irányba való mozdíásánál lesz változás, tehát, ha veszünk egy ablakot és mozgatjuk egy képrészlet fölött és minden irányban lesz változás akkor megkaptuk a sarokppontunkat. Ugyanakkor ez nagyon sok számítást ígényel.

E helyett ha tudunk egy speciálist irányt keresni amelyhez képest minden iráynba a változás értéke nagyobb akkor az egy sarokpont lehet.

Ha u és v a két irány amiben tologatjuk az abalkaot akkor az elmozdított - eredeti négyzetének összegét határozzuk meg: E(u,v) = SUM(I(x+u,y+v) - I(x,y))^2. Keressük azt az u, v értéket amiree elég nagy a hibaérték. Az összegzés belső részét Taylor sorba fejtjük, hogy könyebben kezelhető legyen. Az u,v értékek picik. Ezt egy Hesse féle mátrixnak nevezhetjük. A mátrixhoz rendelhető kisebbik sajátérték az a legkisebb változás mértékét adja meg, a kisebbik sajátvektor a változás irányát. A nagyobbik a legnagyobb változás irányát és értékét.

1. kiszámítjuk a hibaértéket tetszőleges elmozdulással, nem midnen lehetséges u,v-re, hanem a lambdaa-sajátérték egyjellemzőpont lehet.
2. a kép mindne pontjában kiszámoljuk az Ix, Iy értéket, és a H mátrix, sázmunkra fontos argumentumait.
3. megkapjuk az egyenlet megoldását, és a kisebbik érétknél megjelöljük a pontot, és leheetőleg ezekből a legnagyobbat tartjuk meg.

Harris operátor

A két sajátértékből kaphatjuk: f = (lambda1*lambda2)/(det(H)*mátrixnomya(H))ahol a mátrixnomya(H) = h11+h12.

Sarokpont detektálás - Morovec operátor

4x4-es képrészleteket veszünk ki a képből, és vesszük a vízszintes, függőleges, és két átlós éréték minimumát, és kiszámoljuk az ablakokra külön-külön a varianciát, azaz a szórásnégyzeét. Ekkor ha egy 12x12-es tartoányt használunk láthatjuk, hogy hol van az adot területre eső sarokpont.

Sarokpont detektálás - Kanade - Lucas - Tomasi algoritmusa

A mátrix deredmináns érétéékéhez hozzáadjuk a főátlók összegét, és összehasonljtjuk egy treshold értékel.

EA 5 - vonalak detektálása

előzetesen feltételezzük, hogy éldetektálást végzünk, és vannak különálló pixeleink amiket meghatároztunk

cél: az E(x,y) képen találjuk meg a vonalakat és határozuk meg azok egyenletét

Hough transzformáció

COMP 4900D - Hough Transform

kulcs: használjunk paraméterekt ahol a bonyolult probléma az egyszerűbb lokális maximumok megtalálását jelenti

input: nináris kép képpontokkal

Meredekség értékékeben gondolkodunk, megtalálunk egy élpontot, arra meredekséget tételezünk fel, arra vannak m értékei és koordinátái, amire behelyettesítünk x,y-t, ez alapján kapunk b=-mx+y jelleggel.

1. Az (m,b) teret osszuk fel egy rácsalés mindenhez rendeljünk egy számlálót c(m,b) kezdetben 0 értékkel => bi=y-mjx
2. minden élpixel ismert koordinátáival számoljuk ki ab értékétminden lehetségesm` mellett
3. növeljök =c(mi,bi)`-t egyel
4. keressünk lokális maximumokat a képen

kvantálás:

! kvantálás

A művelet viszont 3 egymásba ágyazott ciklus, a számítási jgény kisebb, viszont az x,y tengelyen 0-tól végtelenig vehetünk fel értékeket amihez elég angy memória kell.

Az egyenes egynelet nem csak Descartesi de polár koordinátával is leírható, így a tengely meredekséget vesszük figyelembe, hogy milyen szöget zár be a függőleges tengelyel. Másik kérdés, milyen messz eszerepel az origótól (bal felső saroktól). Ez alapján az egens egyenlete: xcosA + ysinA = p

Ez alapján akkor van legközelebb az oigóhoz, ha átmegy rajta, azaz 0 az értéke. A legtávolabbi pont a főátló vége, azaz a kép mérete. A szóbajövő rtékeket 0 és a képátló méretével kell tehát elheyezni sé nem 0 és végtleen között.

1. készíünk egy 2D számláló tömböt a szög és a 180 fok változik, a távolság pedig a maximum képátló.
2. mindne szög értkére behelyettesítünk valamilyen nvekményt használva (pl 10 fok)
3. számoljuk ki minden élpontra a p értéket, minden kiszámolt (A,p) párra növeljük a sázmlálótömb értékeit.
4. keressünk lokális maximumot.

Ez lokális maximumot és csomósodást fog adni válaszul a paramétere térben. Tehát nagyon zajos kép esetén jelentős hiba állhat fenn.

Nehézségek

• paraméter tér felosztása, nagy felosztással nehéz különbséget teni a vonalak között, kicsivel a zaj okoz gondot
• hány vonalat látunk
• melyi kélpont melyik vonalhoz tatozik?
• zaj miatt nehéz kielégítő megoldást adni

Kör illesztése

három ismeretlen: (x-x0)^2 + (y-y0)^2 - r^2 = 0

• 3D akkumulátor tömböt kell készíteni, dimenziók: x0, y0, r
• lokális maximumot kereesünk A tömbben

gyakorlatban javasolt módszer	példák

Képpiramisok

https://regi.tankonyvtar.hu/hu/tartalom/tamop412A/2011-0063_15_gepi_latas/ch07.html

• Ha az objektumok képe túl kicsi, vagy nem elég kontrasztos, akkor általában nagyobb felbontással vizsgáljuk azokat
• Ha nagy méretűek, vagy kontrasztosak, akkor elegendő durva felbontás
• Ha mind kicsi, mind nagy, illetve alacsony és nagy kontrasztú objektumaink egyaránt vannak a képen, előnyös lehet különböző felbontással vizsgálni azokat
• A képpiramis olyan hatékony és egyszerű képreprezentáció, aminek segítségével a kép több felbontását használjuk

Más elnevezés: Felbontás hierarchiák (Resolution hierarchies)

Skálázás

a képek méretének csökkentése a cél, minden lépésben fele méretű legyen, a környező pixeleket valamilyen interpolációval elhagyjuk, majd vissznagyítunk pl bezie splineokat használva.

kicsinyítés	vissza nagyítás

Cél: képek tömör reprezentációja, gyors algoritmusok készítése

A képpiramisok (= felbontás hierarchiák) a kép különböző skálázású másolataiból épülnek fel

• A piramis minden szintje az előző szint 1/4-e
• A magasabb szint magasabb felbontást jelent
• A legalacsonyabb szint a legkisebb felbontású
• (Megjegyzés: néha a szintek azonosítása éppen ellentétes e kijelentésekkel)
• A magasabb szint pixelértékeit “redukáló” (Reduce) függvény segítségével számoljuk gl= REDUCE[gl+1]

képpiramis működése	algorimtus maga

Piramisok készítése

1. Minden szinten van egy közelítő képünk és egy különbség (maradék) kép
2. Az eredeti kép (amely a piramis alapja) és az ő P közelítései a közelítő piramist építik fel
3. A maradék outputok a “maradék piramist” építik fel
4. Mind a közelítő, mind a maradék piramisok iterációs módszerrel határozhatóak meg
5. A P+1 szintű piramis a konstrukció algoritmusának P alkalommal történő futtatásakor keletkezik
6. Az első iterációban az eredeti 2J x 2J méretű kép az input
7. Ebből készül a J-1 szintű approximációs és a J szintű maradék eredmény
8. Az iterációk során az előző iteráció eredményét használjuk az új lépés inputjaként

Minden iteráció három lépésből épül fel:

1. Számoljuk ki az input kép redukált felbontású közelítését. Ez szűréssel és pixelek leosztásával (downsampling by factor 2) történik
   • Szűrő: szomszédok átlagolása, v. Gauss szűrő, stb.
   • A közelítés pontossága függ a szűrőtől (lásd később)
2. A kapott output pixeleinek felszorzásával (upsampling by factor 2) és szűréssel készül a közelítő kép, aminek a felbontása megegyezik az inputéval.
   • A pixelek közötti interpolációs szűrő meghatározza, hogy mennyire jól közelítjük az inputot az 1. lépésben
3. Számoljuk ki a 2. lépésben kapott közelítés és az 1. lépés inputjának különbségét (maradék). A különbség később az eredeti kép rekonstruálásához használható

Alkalmazási területek

• Hasonló részek keresése
• Keressünk durva skálán, majd finomítsunk nagyobb felbontásnál
• Élkövetés, mozgások vizsgálata
• Minták keresése
• Csíkok keresése
• Nagyon fontos textúrák vizsgálatánál

Gauss piramis 1D-ben

• szimetrikus konvolúőciós maszk: [w(−2),w(−1),w(0),w(1),w(2)]w(i)=w(i)⇒[c,b,a,b,c]
• A maszk elemeinek összegea+2b+2c=1

Minden csomópont egy adott szinten ugyanannyi összsúllyal járul hozzá a következő szinthez:

Konvolúciós maszkok (5 × 1)

képpiramis működése	algorimtus maga
	a = 0.4 - Gauss maszk a = 0.5 - háromszög maszk a = 3/8 - könnyen számolható maszk

Laplace piramis

• Hasonló az élszűrt képekhez
• A legtöbb pixel 0
• Tömörítésre is használható
• Laplace piramis orientáció független

Laplace piramis készítése:

Gauss piramis kiszámítása: gk,gk-1,gk-2,...g2,g1

Laplace számítása: Gauss – „visszahízlalt (Expand) előző Gauss”

Lk   =gk−EXPAND    (gk−1)
Lk−1 =gk−1−EXPAND  (gk−2)
Lk−2 =gk−2−EXPAND  (gk−3)
⋮
L1   =g1

Képrekonstrukció piramisokból

• Az eltárolt piramisokból az eredeti kép visszaállítható
• A Laplace piramis jól tömöríthető (a kép homogén részeinél)

g1=L1g2 =EXPAND  (g1)+L2
g3      =EXPAND  (g2)+L3
⋮
gk      =EXPAND  (gk−1)+Lk

Textúra transzfer

• Készítsük el a narancs kép Laplace piramisát (Ln)
• Készítsük el az alma kép Laplace piramisát (La)
• Készítsük el a következő összemásolt Lc piramist:
  • az alma La piramisának bal részét minden szinten és a narancs Ln piramis jobb oldalát minden szinten másoljuk egybe
• Rekonstruáljuk a kombinált képet Lc-ből

transzformációk:

https://wiki.tum.de/display/lfdv/Spatial+Transformer+Networks

Mindig az a kérdés hogy a világhoz viszonyítunk (globális koordináta) és a lokális rendszer csak elszenvedi a történéseket vagy lokális koordináta rendszerben vagyunk.

1.Eltolás (transzláció) 2.Forgatás (rotáció) 3.Skálázás 4.Elferdítés

• Képeket sokszor egymásba kell transzformálni (warping)
• Koordinátarendszereket is gyakran egymásnak meg kell feleltetni
• A kamera és a kép, valamint a kamera és a világ koordinátarendszerek között is kapcsolatot kell teremteni

Erre keresünk hatékony reprezentációt

• 2D pont közönséges koordinátái: 𝐏=[𝑥,𝑦]𝑇
• Homogén koordinátákkal: 𝐏=[𝑠𝑥,𝑠𝑦,𝑠]𝑇 ahol s a skálázófaktor

Áttérés koordinátarendszerek között

• Egy kép pontját egy másik kép pontjának szeretnénk megfeleltetni
• Lokális koordinátarendszerben adott pontot, világ koordinátákba szeretnénk átképezni
• A művelethez egyszerű mátrix-szorzást szeretnénk használni
• Adott P pont, és az M transzformáció segítségével megkapjuk a pont P leírását a másik koordinátarendszerben:𝐏=𝐌𝐏′

Skálázás mátrix-operációként

• 𝐏=[[𝑠𝑥, 0][0,𝑠𝑦]]𝐏'
• origóhoz képest nyújtás: [x,y] = [[𝑠𝑥,0][0,𝑠𝑦]][𝑥′,𝑦′] = [𝑠𝑥∙𝑥′, 𝑠𝑦∙𝑦′]
• forgatás síkban: [𝑥,y]=[[cos𝜃, −sin𝜃][sin𝜃, cos𝜃]][𝑥′, 𝑦′] = [[𝑥′, cos𝜃−𝑦′sin𝜃][𝑥′, sin𝜃+𝑦′cos𝜃]]
• Eltolás (transzláció): [𝑥, 𝑦, 1] = [[1, 0, 𝑥0],[0, 1, 𝑦0],[0, 0, 1]] [𝑥′, 𝑦′, 1] = [𝑥′+𝑥0, 𝑦′+𝑦0, 1]
  • 𝐏 = 𝐌𝐏′, ahol homogén koordinátás leírást használunk
  • 𝐏 = [𝐈, 𝐭]𝐏′ ahol Iaz identitás, egységmátrix
• Euklideszi transzformáció:
  • Eltolás és forgatás egy időben
  • 𝐑 forgató almátrix, 𝐭 eltolás oszlopvektor
  • 𝐏=[𝐑, 𝐭] 𝐏′
  • `𝐑 = [[cos𝜃, −sin𝜃][sin𝜃 cos𝜃]]
  • `[𝑥, 𝑦, 1] = [[cos𝜃, −sin𝜃, 𝑥0][sin𝜃, cos𝜃, 𝑦0][0, 0, 1]][𝑥′, 𝑦′, 1]

EA 6

homogén koordinátás rendszer

• hol az origó
• hol az átvezető rész, hogyana alakul az átvezetés

forgatás

elemi forgatás

két értéke van:

• egy tengely körül (x,y,z)
• a forgatás mértéke

pl: *x tengely körül g szögben:

            1   0     0    0
            0 cos g -sin g 0
rot(x,g) =  0 sin g  cos g 0
            0   0     0    1

transzformációk

• 3D -> 2D
• modellek kezelése
• gépi látás: kamera egy koordináta rendszer, sík egy másik,

Ha van egy test amit le szerettnénk írni akkor vannak pontok amiket kezelünk, és az obketrum felületét adjjuk meg , pl háromszögekkel kifejezni az objektumot. Ígí a háromszög csúsából megmonható, hogy hol van, és akkor a háromszög csúcsából megmondható, hogy látjuk-e vagy sem az adott szögből.

viszonylag jól tudunk dolgozni ha van n csúcs, ekkorr egy 4*nes mátrixba tudkuk betenni. Ha mozgatjuk, megszorozzuk balról egy 4*4-es mátrixal. Megindexeljük a csúcspontokat, n oszlopa van n csúcs esetén. objektum leíró mátrixot szorozzuk egy 4*4mátrixal.

EA 7

Képoperációk osztályozása

Hisztogram:

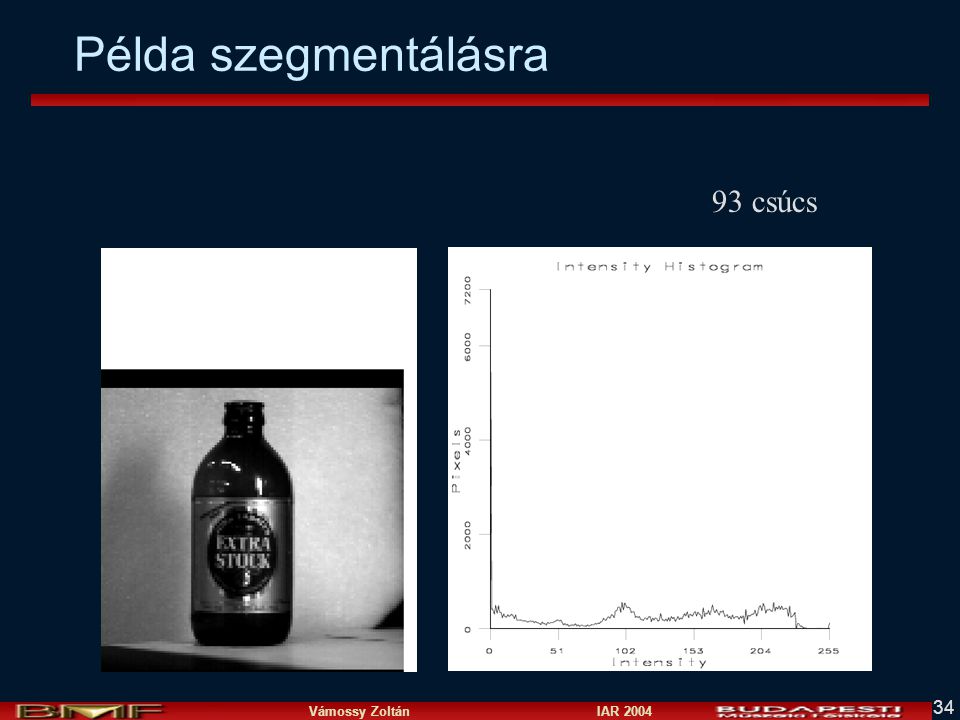
Olyan grafikon ami minden lehetséges szürke árnyalathoz megadja a képen az adott árnyalatú pixelek számát.

Ha normalizáljuk (minden értéket elosztunk a kép méretével), akkor az egyes pixelértékek előfordulási valószínűségét kapjuk.

küszöbértékek meghatározása

• mindig zajszűrésszel érdemes kezdeni
• lehet manuálisan megadni, ha pl jól elkülönül a háttér és a világítás.
• adaptív eljárások melyek az inpput képhez automatikusan választják az optimális küszöbértéket
  • lehet globális érték, medián mentén, vagy átlagolva, isodata algoritmus.
  • ha egyenetlen az objetum akkor egy lokális módszer jobb lehet: Niblack algoritmus

Több küszöb szerint is szétvághatunk, erős csúcsok, mély elválasztó völgyekkel segítenek.

Ha tudjuk, ohgy az objektum hányad részét foglalja el, tehát a tárgyhoz tartozó pontok a telejs képhez képest p-ed rész, akkro a tárgyhoz tartozó pontok aránya 1/p Ehhez választunk egy T küszöb értéket:

Hiszterézisses küsszöbölés: ha nincs tiszta völgy a hisztogramban akkor a háttérben sok olyan pixel van aminek az intenzitása megyezk az objektum pixeleinek intenzitásával és fordítva.

• két küszöböt definiálunk a völgy két végén.
• A nagyobb küszöb feletti pixelek objektumok, a kisebb alatti háttér
• A két küszöb közötti akkor objektum, ha létezik objektumhoz tartozó szomszédos pixele

Isodata algoritmus - Yanni

Jól használható, ha az előtér és a háttér kb. ugyanannyi pixelből áll. Egy olyan iterációs technika ahol kezdetben kiindulunk egy értékből, amit szétbontunk az aktuálsi pillanatokban vett érték intenzitásokra, kiszámoljuk ezek átlagát, a két átlagban súlyozva határozzuk meg az értéket addig amíg nincs érdemi változás.

• Inicializálás: a hisztogramot két részre osztjuk (célszerűen a felezőponton): T0
• Kiszámítjuk az objektum, valamint a háttér intenzitásának középértékét: TO, TB (küszöbnél kisebb intenzitásúak, ill. nagyobbak átlaga)
• Az új küszöbérték a két középérték átlaga: Ti=(TO+TB)/2 – Vége: ha a küszöbérték már nem változik: Tk+1=Tk

Otsu algoritmus

A bemeneti kép L szürkeárnyalatot tartalmaz A normalizált hisztogram minden i szürkeértékhez megadja az előfordulás gyakoriságát (valószínűségét): pi

• Az algoritmus lényege: keressük meg azt a T küszöbszámot, amely maximalizálja az objektumháttér közötti varianciát (szórás négyzetet).
• Homogén régiónak a varianciája kicsi
• Bimodális hisztogramot tételez fel

A háttér súlya egy általunk nem ismert T küszöbig való összegzés, kiszámoljuk a háttér, az előtér és a középérték teljes érétkét amit megtehetünk az objektumra is. A középértékre nézett eltéréseket figylejük, ami a szórást adja meg.

	Ha ismerjük valamelyik középértéket a etljes képre, meg az objektumra, háttérre vonatkozóan, akkor akár
Ezt a teljes képre is kisázmolhatjuk, ami felbontható 4 tagra, amiből 2 tag ami az osztályon belüli variancia ami a háttér szórásnégyzetét adja meg és a másik 2 tag az osztályok közötti érétket befolyásolja. Keressük azt a T küszöböt amire a második rész, az osztályok közötti szórásnégyzet lehet nagyobb.	Ezt módosíthatjuk, ha az egyes osztáylok varianciáját számoljuk és azok miniumával megadhat az osztályok közötti variandia maximuma. Bizonyítható, ohgy ez monoton növekvő.

Lokálisan változó küszöbölés

Ha nem a teljes képre hanem a képet felbontva részegységekre számoljuk ki a fenti módszereket akkor javíthatjuk a végeredményt. Előnyös ha a háttér nem homogén. Hátránya, hogy mivel az adott kis cellához mérünk mindent akkor igazából olyan helyeken ahol nincs jelentős változás a képen eltűnhetnek elemek, vagy épp ghost objektumok jelennek meg.

Dinamikus lokális küszöbölés

Nibblack algoritmus

Egyetlen küszöb nem legendő az bojektum és a háttér szétválasztásához. Változó küszöbérték T(i,j) kell, amely követi az intenzitásváltozást.

Posztptprocesszinget érdemes elvégezni a gradiens értékét figyelembe véve.

Szegmentálás

Régió szegmentálás lehet egy háttérből kiemelés, vagy réteg reprezentációhoz, ahol külön rétegekre bontjuk a kép elemeit. Lehet a teljes képet egy fa szerű hierarchia rendszerbe is felbontani.

Hasonlósági feltételek

• A részkép minden pixele ugyanolyan intenzitású
• Bármely részképben a pixelek intenzitása nem különbözik jobban egymástól, mint egy adott küszöb
• Bármely részképben a pixelek intenzitása nem különbözik jobban a régió átlagos intenzitásától, mint egy adott küszöb
• Bármely régióban az intenzitásértékek szórása kicsi

A szegmentálás sikeres ha

• a régiók homogének és egyenletesek (uniformitás),
• a régiók belsejében nincsenek lyukak,
• a szomszédos régiók között jelentős különbség van,
• a szegmensek közötti határ egyszerű és pontos.
• küszöböléses (lásd korábban is)
• él-alapú
• régió-alapú
• illesztésen alapuló

Él-alapú szegmentálás

https://regi.tankonyvtar.hu/hu/tartalom/tamop412A/2011-0063_15_gepi_latas/ch08.html

• A hisztogram csak a szürkeségi értékek előfordulási gyakoriságát mutatja meg, a pozíciók, a szomszédos elemek szürkesége és egyéb információk hiányoznak.
• Ahhoz, hogy zárt és összefüggő határvonalakat kaphassunk más módszerek szükségesek.
• Előforduló problémák (pl. zaj esetén):
  • álpozitív (false positive) élek — élt detektálunk ott, ahol nincs él;
  • álnegatív (false negative) élek — nem találunk élt, pedig van

1. kép símitás
2. él korrekciós módszer laklamazása
3. élek kapcsolása, csoportosítása

Él korrekciós módszerek

Él relaxáció

• egy él akár erős is ha nincs folytatása a környezetében valószínűleg nem tartozik semilyen határshoz
• egy gyenge él, ha két erős él között van, valószínűleg a határvonalhoz tartozik

Él kapcsolás

• Összekapcsolhatunk szomszédos él-pontokat, ha hasonló tulajdonságaik vannak:
  • Hasonló a gradiensük nagysága valamely küszöbértékre
  • Hasonló gradiensük iránya valamely küszöbértékre

Régió alapú szegmentálás

• az objektum/szegmens által elfoglalt területet határozza meg.
• Megközelítések:
  • régió növelés (region growing)
  • egyesítés (merge)
  • szétválasztás (split)
  • egyesítés és szétválasztás (split & merge)
  • fagocita algoritmus

Seed segmentation lépései:

• Számítsuk ki a kép hisztogramját
• Simítsuk a hisztogramot átlagolással vagy Gauss szűréssel (kis csúcsok, zajok eltüntetése)
• Detektáljunk “jó” csúcsokat (peakiness) és völgyeket – lokális maximumok és minimumok keresése-, peakiness test
• Szegmentáljuk a képet bináris képpé a völgyben lévő küszöbökkel (rendeljünk 1-t a régiókhoz, 0 a háttér)
• Alkalmazzuk a kapcsolódó komponensek algoritmusát (connected component algorithm) minden bináris képrészre, hogy megtaláljuk az összefüggő régióka

https://www.inf.u-szeged.hu/~gnemeth/kurzusok/kepfel1/matlab_resz/12_gyakorlat.pdf

Rekurzív kapcsolódó komponens módszer - Connected Component Algorithm - Dolgozzuk fel a bináris képet balról jobbra, fentről lefelé - Ha még nem címkézett 1-t tartalmazó pixelhez érkezünk, akkor rendeljünk egy új címkét hozzá - Rekurzívan vizsgáljuk meg a szomszédait a 2. lépésnek megfelelően, és rendeljük hozzá ugyanazt a címkét, ha még nem címkézettek és az értékük 1 - Álljunk meg, ha minden 1 értékű pixelt megvizsgáltunk - Megjegyzés: 4-es, 8-as szomszédság

Soros kapcsolódó komponens módszer

1. Dolgozzuk fel a bináris képet balról jobbra, fentről lefelé
2. Ha még nem címkézett “1”-t tartalmazó pixelhez érkezünk, akkor rendeljünk hozzá egy új címkét a következő szabályok szerint:

  0      0      0       0
0 1  ->  0 L    L1 -> L L

  L      L      L       L
0 1  ->  0 L    M1  ->  M L       (L=M)

3. Határozzuk meg a címkék közül az ekvivalenseket (pl.: a=b=e=g és c=f=h, és i=j)
4. Az ekvivalens csoportok minden eleméhez rendeljük ugyanazt a címkét második körben

továbbfejlesztése

• A kis régiókat kapcsoljuk nagyobbakhoz – Régió növelés
• Nagy régiók szétvágása – Régió vágás
• Gyenge határok eltüntetése szomszédos régiók esetében

Régió növelés

• Régió vágás és egyesítés (split and merge)
• Fagocita (phagocyte) algoritmus
• Valószínűségi arány teszt

Split and Merge régiókra

Split and merge esetén nem biztos hogy ugynaazt kapjuk mindkét irányból iindulva.

Vágás: vágjuk a nem homogén régiókat 4 szomszédos részre

• Egyesítés: hasonló tulajdonságú (uniform) szomszédos régiókat kapcsoljuk össze
• Álljunk meg, ha már nem lehet sem vágni, sem ragasztani
• Az uniformitás/hasonlóság függvénye: P

Quad Tree

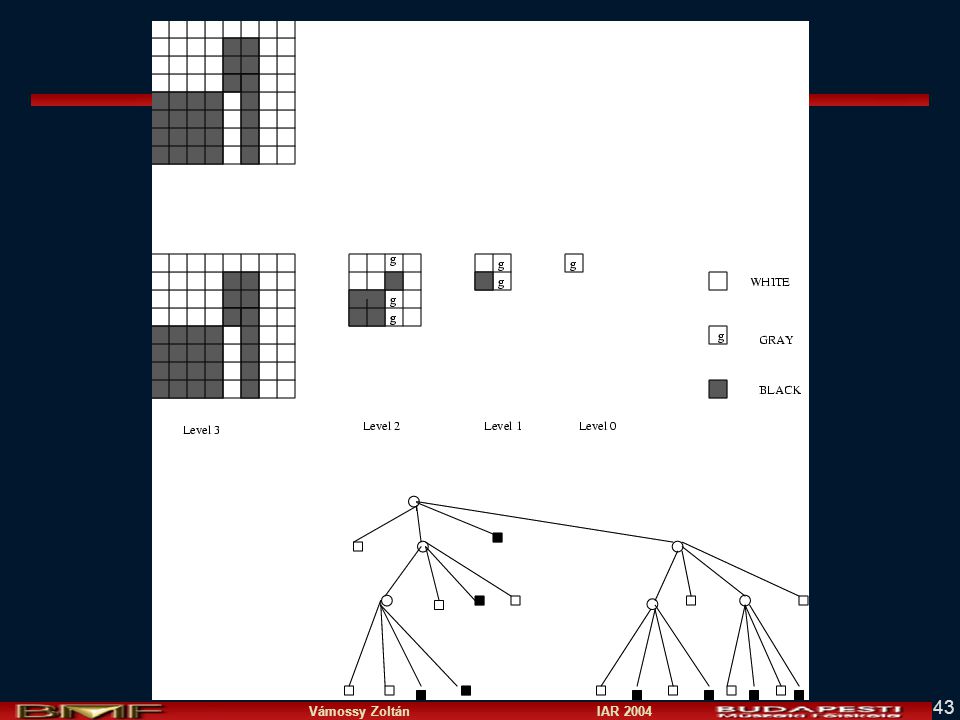
Négyes fa adatstruktúra régióreprezentáláshoz

• Három fajta csomópont: szürke, fekete és fehér
• Elsőként generáljunk egy piramist:
• Ha a piramis fehér, vagy fekete, akkor visszatérés, egyébként: – Rekurzívan keressünk egy quad tree-t X1 negyedben – Rekurzívan keressünk egy quad tree-t X2 negyedben – Rekurzívan keressünk egy quad tree-t X3 negyedben – Rekurzívan keressünk egy quad tree-t X4 negyedben – Return

Faocita algoritmus

határ összeolvastásaára jó, a gynege határokat szüntetik meg az élősködők, í]y nem a régiókra koncnetrálunk, csak a közös területre.

Olyan értékeket keresünk ami ka határ erősségét vagy gyengeségét reprezentálják. Kiveszünk intenzitást a régióból, nem tetszőleges két poontot, hanem a határ mentén levő közös pixelpárokat vizsgáljuk. Ha ezek egy küszöbnél jobban nem térnek el akkor ezt a párkapcsolatot megjelöljük egynullával, egyessel ha nagyobb. Megsázmoljuk hogy poáronként háyn ilyent találtunk összesen.

• összeolvasztjuk a két régiót ha egy küszöbnél kisebb az előbb kapott összeg
• összeolvasztjuk a két régiót ha akapott összeg és a határon levő összes pont számának hányadosa nagyobb mint egy küszöbérték.

Valószínűségi arány teszt

A kérdés ugyanaz: összeragasztható-e a két régió. Az egyik régió R1 a másik R2, és ehhez számolunk szórást és intenzitás eloszlást. Ehhez megnézzük, hogy a másik régióban vett elemek intenzitása milyen valószínűségben vannak. A két régiós hipotézist és az egy régiós hipotézist is kiszámoljuk, és megkapjuk, ohgy melyik teljesül, azzal, hogy kiszámopljuk a hányadosukat.

Ezt kiegészíthetjük egy Régió szomszédsági gráf-al:

• Régiók reprezentálására jól használható adatstruktúra
• A régiók csomópontok a gráfban
• Az élek a régiók szomszédságát reprezentálják
• A gráfban kell csak a csomópontokat „adminisztrálni”: azonosság jelzése; majd eltávolítás

Régió szegmentálás és éldetektálás összehasonlítása

• Zárt határ – Éldetektálás esetében általában nem – Régiószegmentálás zárt határokat produkál
• Lokális < > globális – Éldetektálás lokális művelet – Régiószegmentálás globális
• Jellemző vektorok tulajdonságainak növekedése – Általában nem javítja az éldetektálás hatékonyságát nagy mértékben – Javítja a szegmentálás hatékonyságát (mozgás, textúra, stb.)
• Határpontok – Pontos helyzet meghatározás az éldetektálás során – Általában nincs ilyen

EA8 - Invariáns leírók

Leírási módok:

• régió határaihz kapcsolódó jellemzőkkel, ha a régió alakján van a hangsúly
• régió belső jellemzőivel (textúra, szín, stb)

Külső leírók:

• http://www.inf.u-szeged.hu/~kato/teaching/DigitalisKepfeldolgozasTG/11-ShapeDescriptors.pdf

Lánckód

bőveben: https://regi.tankonyvtar.hu/hu/tartalom/tamop412A/2011-0063_15_gepi_latas/ch09.html

Körbejárjuk az objektum határát amíg körbe nem érünk, az egyes lépések irányait kódoljuk.

• Iránykódot rendelünk minden pixelpárhoz
• kövessük a htárt az óramutató járásának irányában.
• ha zaj megjelenik a kpen akkor az az objektumok határán is megjelnik. Valamennyire invariáns a lánckód, de nem teljes mértékben. Nem jó a forgatás, ha relatív irányban gondolkodunk. A lánckód nagyon hosszú lehet. Gyakorlatban nem túl hatékony megoldások, poligonokkal való közelítés jobb lehet.

pl:

Általában két különböző felosztást különböztetünk meg, a 4 és a 8 irányú felosztást:

Ekkor ha van a következő képünk, aminek az alábbiak a határpontjai:

Akkor miután mintavételeztünk a pontokból, hogy ne mindet használjuk, minden egyes maradék pontra ráillesztjük ezt a fenti "csilagot":

Tehát a kapott lánckód a bal oldalon, a 4 ágú csillaggal, ha a legfelső bal oldali pontból indultunk el: 0033333323221211101101

Differenciált lánckód: Tekintsük körkörös sorozatnak a lánckódot és számoljuk ki a differenciákat két egymás utáni elemre vonatkozóan, azaz az egymást követő elemek különbségét képezzük (modulo 4 vagy 8), így az egymást követő irányok változását tárolhatjuk el. pl: 4 ágú "csillagra":030000031303130031013

Alakszám: a differenciák körkörös sorozatában a legkisebb egész szám, ez a kiindulóponttól való függés megszűntetése miatt előnyös. pl: 000003130313003101303

• n-ed rendű alakok: n elemű lánckóóddal elírható zárt alakok lehetséges fomái pl:

lánckód 003221

Módosított alakszám

1. rögzítsük az alakszám rendjét.
2. határozzuk meg a fő és melléktengelyt és azok irányát
3. határozzuk meg a minimális befogadó téglalapot melynek alakszám rendje = n és oldalainak aránya = excentricitás
4. számoljuk ki az alakszámot ebben a rácsban.

Szignatúra

• határon haladva az ót függvényében az érintő iránya egy refeernciához képest
• meredekség sűrűség függvény: érintőfüggvény hisztogramja
• az egyenes szegmensek csúcsok lesznek a hisztogramban

Mi a négyzet szigantúráában az átfogó értéke a szög függvénéyben? Milyen szigaantúrák vannak? Mi az alakszám rendje?

Fourier leírók

• Adott N pontból álló rendezett határ: (x0,y0),(x1,y1)...(xY-1,yN-1)
• minden koordinátát kezeljünk komplexként s(k) = xk+j*yk
• a(u) = 1/N*sum(s(k)exp(-j2PIuk/N))
  • u : 0..n-1
  • a komplex értékek Ha N lemeből áll a kontúrsorozat akor a furier leírók sázma is N. Elhagyjuk a magas fekvenciás tagokat, amik a kis változásokat jelentik, az alacsony frekvenciák a durva görbületeket határozzák meg.

Régió tulajdonságok

Terület

pixelek száma a régióban

Tömegközéppont/súlypont

Képek értékét osztjukk a területtel

Nyomatékok, momentumok, inerciák

centrálásra, forgatásra invariánsok:

Kerület

A régió határán lévő pixelek száma. Megj: néha másképpen értelmezik: 1 és gyök2 távolságok összege.

kompaktság

elem kerülete/4*PI*terület => kör kompaktásga = 1

orientáció

A nyomatéki főtengelyt, vagy inercia tengelyt adja meg.

Az egyenestől vett távolságokat kezeli. Azo ka tengelyek melyek sézlsőérétkei, minimumai az értáknek azok az inercia negelyek.

A főtengelyre merőlegeseket mérünk fel és azok távolságát nézzük a koordináta tengelyektől.

• nyomatéki főtengelyek aránya
• topolgiai leírók
• textúra

Optikai folyamatok alkalmazása

EA9 - Arcfelismerés - detektálás és authentikáció

AdaBoost

Képpont intenzitások összege a kép egy részén (fekete) - Képpont intenzitások összege a kép egy másik részén (fehér)

****
****
****
    ****
    ****
    ****

Sorösszegeket veszünk mindegyik sötét és világos részhez, így kapjuk az integrál képet. Ezeket több méretben futtatjuk a képen, hogy különböző méretű arcokat is megtaláljon.

kaszkádba szervezés: jellemző detektorok hierarchiába szervezése, ha a nagyobb méretű azt jelzi, hogy nem illeszkedik értelmetlen a pontosításokat tesztelni, hiszen úgysem arc.

pl:

Gazdag ember (RP) szakértőkből 50 fős csapatot akar összeállíani. Ehhez az elmúlt öt évre 10000 szakértő teljesítményét nézi. => 1000 nap mert minden évben 200 napig vna nyitva a tőzsde. Megkérdezte a szakértőket, hogy adott nap x ponttal nőni vagy csökkeni fog-e az árfolyam. Tehát igen/nem típusú értékeink vannak.

• Első helszre nyilván azt választjuk a ki legtöbb helyes választ adja.
• Scharpire ötlete alapján a második kiválaszott szakember az aki az első hibázási alkalmainál a legtöbb helyes választ adja. És így a 3., stb elyre is. Ők a gyenge szakértők, akik elég jól kiegésítik egymást.

Így olyan csapatot tudunk összeállítani, amivel az össz értéke, össz helyes válaszok aránya magas lesz. FONTOS: aki pont 50%-on áll az nem alkalmazható, mert semmilyen komplementer halmlazoz nem ilelszhető jól!

Ezek után beállítjuk, hogy melyik szakértő véleményét hány százalékban vesszük figyelembe, ezek a súlyok. Ez a helyes válaszok számától függ mondjuk.

Tréning fázis

Sok képen próbáljuk ezt a fekete-fehér abalkozást. Az ablakok a szakértők. Ezt kipróbáljuk arcokon és nem arcok is! A szakértők válaszait tároljuk, hogy megmondhassuk melyik szakértő mennyire számít.

Minden képre kapunk egy-egy valséget minden szakértőtől, hogy az arc-e vagy sem. DE minden szakértőről tudjuk, hogy mennyire megbízható a véleméyne, ez az ő súlya. A szkaértők összsúlya 1 Ezek alapján megmondhatjuk, mennyire számít a véleménye az adott képpel kapcsolatban. A képeknek egy saját súlya keletkezik minden szakértőtől. Ha arc akkor nő a súlya. A folyamat végére megmondhatjuk, hogy a súlyok szerint mely képek arcok.

SVM

Gradiens értékeket számolunk, és az alapján vesszük az irányvvektorok irányát, szögét

A mélytanulási hálók kiszorították ezt a technológiát.

biometrikus azonosítás

• Ismeret alapú megközleítés: vízszintes és függőleges hisztogrammok, de ez csak egy emberre jó!
• Éldetektálással is lehet, ha az éleekből ellipszis alakú vonalakat keresünk.
• Hasonlóan lehet különböző jellemző, vonalakat detektálni

Megjeleneés alaú módszerek:

• szín alapú mdszerek: YCrCb módszerel meg
• Holisztikus módszer: saját arcok
  • pár emberről készítűnk képet amiből képezünk egy átlag arcot
• Gábor wavelet. eltárolunk bizonyos részeket a képeken, és sikeresen detektál a képen jellemző pontokat, ezek nem féltetlen azok a pontok amit emberek is megadnának jellemző pontnak.

Morphing: egyik arc egy másik arcác alakul át, és a köztes lééseket generáljuk le.

3D fejmodell animálás

ZH-ról

• 20-25 perc egymondatos válaszok
• a maradék egy feladat a félév közben vett feladatokhoz hasonlóan.

Gyakorlás ZH-ra

1. Sobel, hisztogram, medián szűrő

/elek_sarok_sobel/

1. Az alábbi kép nyolc lehetséges szürkeárnyalatos intenzitással rendelkezik. Rajzolja le a kép hisztogramját! Hajtson végre a képen hisztogram kiegyenlítést és adja meg a transzformált képet! (2+6 pont)

0	1	5	5	5	5	5	0
1	1	1	4	5	5	5	4
1	0	0	1	6	6	6	4
1	0	0	3	6	6	6	4
1	0	3	3	6	4	4	7
0	0	3	2	6	4	4	4
0	2	2	2	6	4	4	4
0	2	2	2	4	6	4	0

2. Adott egy 10 x 10-es bináris kép a közepén egy 4 x 4-es négyzettel, ahol a pixelek értéke 1, máshol pedig 0. Határozza meg és rajzolja be a gradiens irányát a Sobel operátor alkalmazása után. Határozza meg a kapott pixelértékeket (6 pont). Oldja meg a feladatot mindkét ismertetett távolságfogalom használatával! (4 pont) Hol és mennyiben tér el az eredmény? (2 pont)

3. Legyen f(i, j)= |i-j| i, j = 0, 1, 2, …, 7 egy 8 x 8-as kép. Hajtsunk rajta végig 3 x 3-as médián szűrést (3 pont). A határpixelek ne változzanak!

2.1. Hough Transzformáció - éldetektálás; sarokpont detektálás

/hough-jellemzo_pont/

1. Az alábbi binarizált képen valósítson meg egy Hough transzformációt és ennek segítségével adja meg a két legrelevánsabb egyenest! (10 pont)

0	1	0	0	0	0	0	0
0	1	0	0	0	0	0	0
0	1	0	0	0	0	0	0
0	1	1	1	1	1	1	0
0	1	0	0	1	0	0	0
0	1	0	0	0	1	0	0
0	1	0	0	0	0	0	0
0	1	0	0	0	0	0	0

2. Határozza meg a jelzett területen 3×3 méretű átlagolással összegzett H mátrixának kisebbik sajátértékének meghatározásával, hogy melyik pixel leginkább jellemző pont! (12 pont)

131	133	145	153	163	173
88	90	99	109	115	124
101	106	89	76	81	83
148	162	106	43	23	29
154	158	108	38	35	30
143	153	109	59	64	56

2.2. Egységkocka forgatása

/egysegkocka_forgatas/

1. Egy egységkocka felének kezdeti és célállapotát mutatják az alábbi ábrák. Az objektumot nem lehet átméretezni és az xy sík alá sem lehet mozgatni. (Megjegyzés: A kocka átlós lapjának egyik élhossza gyök(2)).

• Határozza meg az objektum homogén koordinátás leírómátrixát! • Határozza meg azt a transzformáció sorozatot, amely a kezdeti pozícióból a célhelyzetbe mozgatja az objektumot! Számítsa ki az objektum új pozícióját minden egyes elemi transzformáció után! (10 pont)

3. Alakleírók

/alakleiro/

1. Tételezzük fel a következő 8-szomszédságú lánckódot, számoljuk ki az alakszámot: 076666553321212 (6 pont)

64	67	83	122	146	140	142	142
66	73	96	129	146	141	139	143
68	82	101	137	147	140	147	139
70	91	135	147	155	156	151	140
70	95	137	155	156	151	140	143
69	83	141	156	160	156	146	150
68	87	126	153	163	158	152	155
68	88	126	153	164	158	155	155

2. A fenti tömb egy kép intenzitásértékeit tartalmazza. Hajtsunk végre iterációs küszöbölést (Isodata algoritmus) (6 pont). Teszteljük a Niblack módszert is 4 × 4-es ablakméretre (6 pont).

3. Tételezzük fel a következő bináris képet, ahol az egyesek az objektumot jelölik. Határozzuk meg az első kettő Hu-féle invariánst (8 pont), határozza meg a nyomatéki főtengely irányát és rajzolja be a képre (4 pont)!

0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0
0	0	1	1	1	0	1	1	0	0
0	0	0	1	1	1	1	0	0	0
0	0	0	1	1	1	1	0	0	0
0	0	0	0	0	1	1	0	0	0
0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0

4. Egy a oldalú négyzet csúcsával úgy áll, hogy súlypontja éppen az origóban van az átlók pedig az x és y tengelyek irányában helyezkednek el. Rajzolja meg a négyzet szignatúrájának diagramját, ha a vízszintes iránytól indulunk és a szög függvényében a gradiens irányát vesszük fel függvényként! (8 pont)