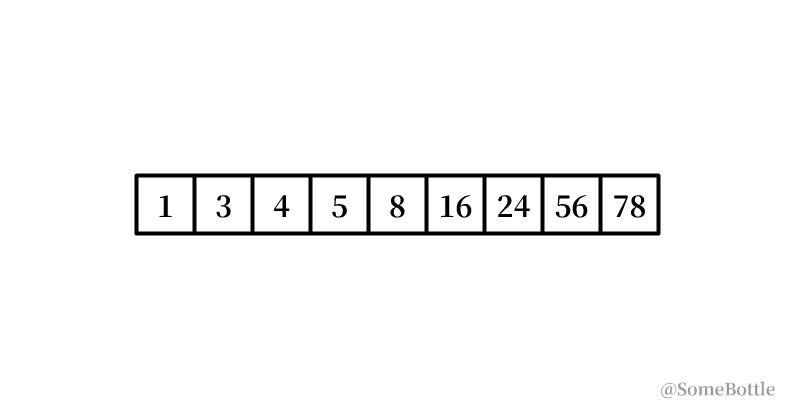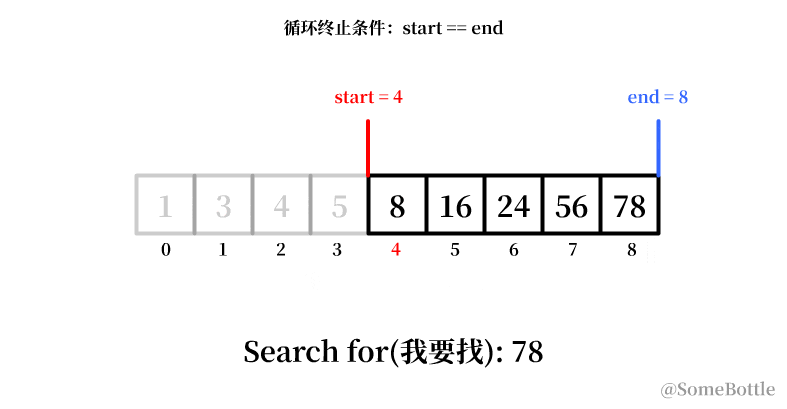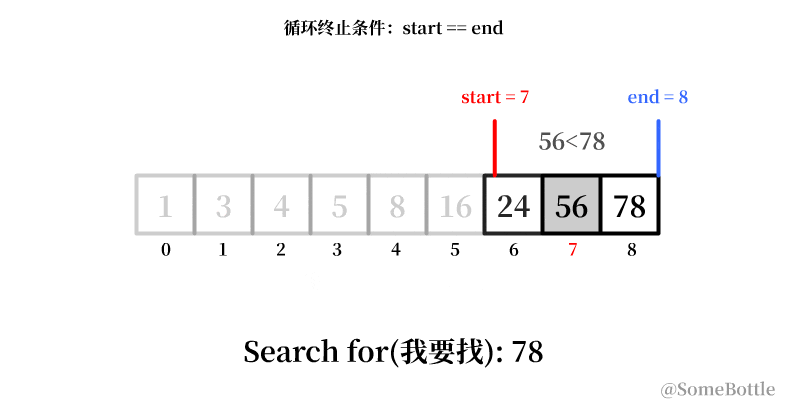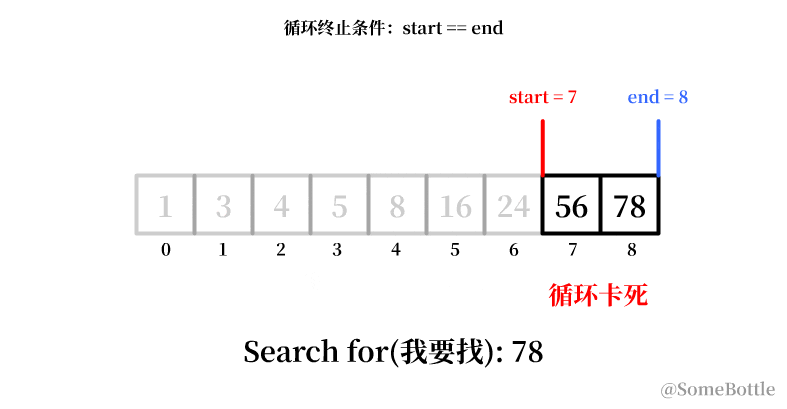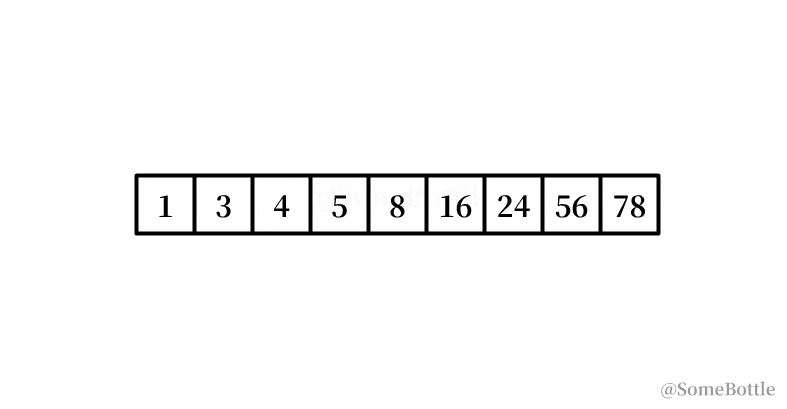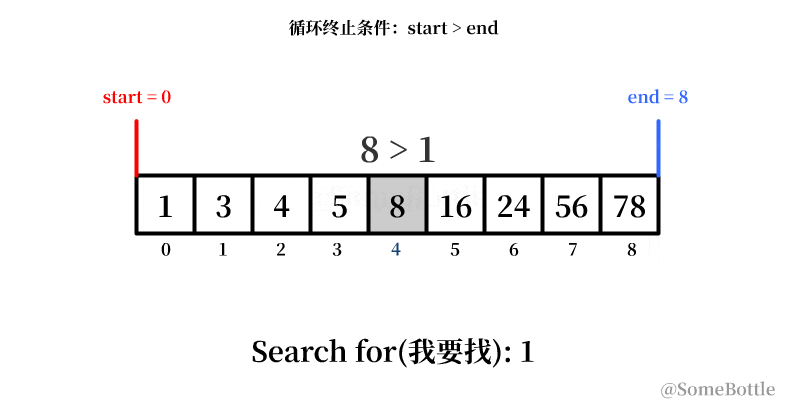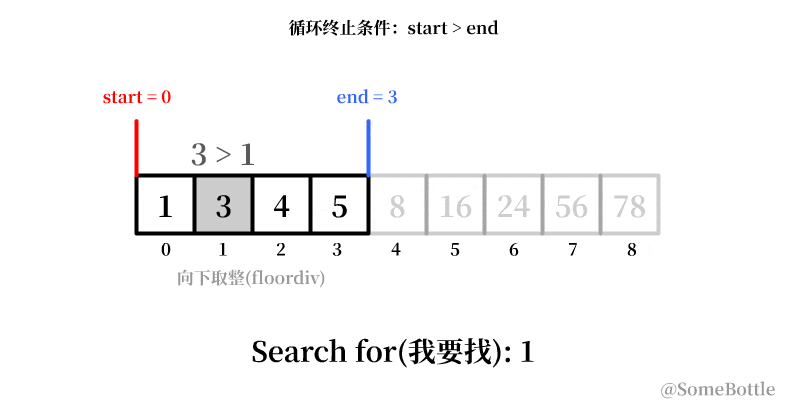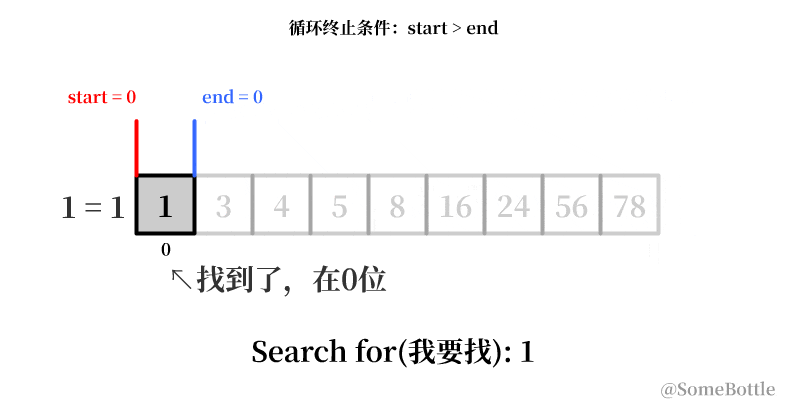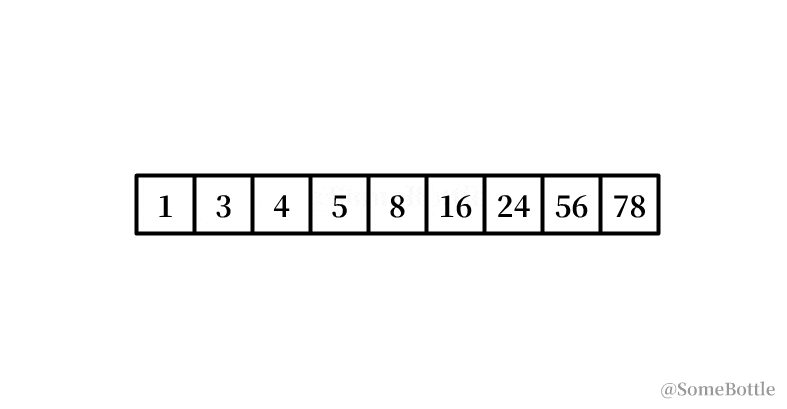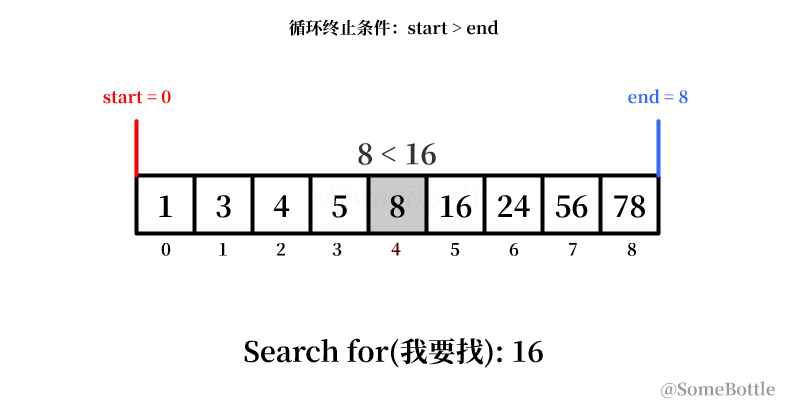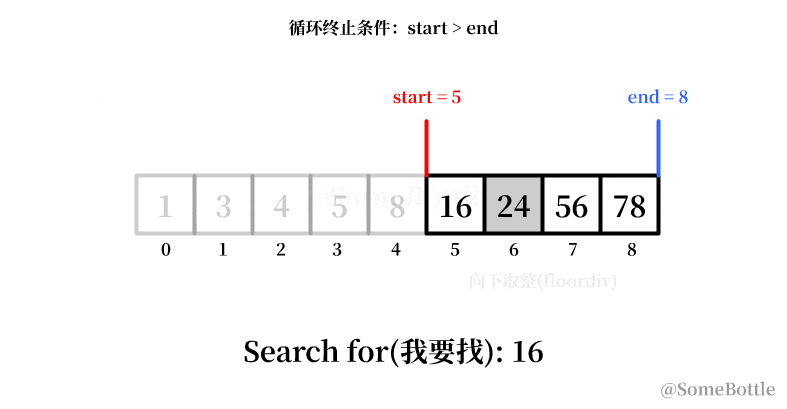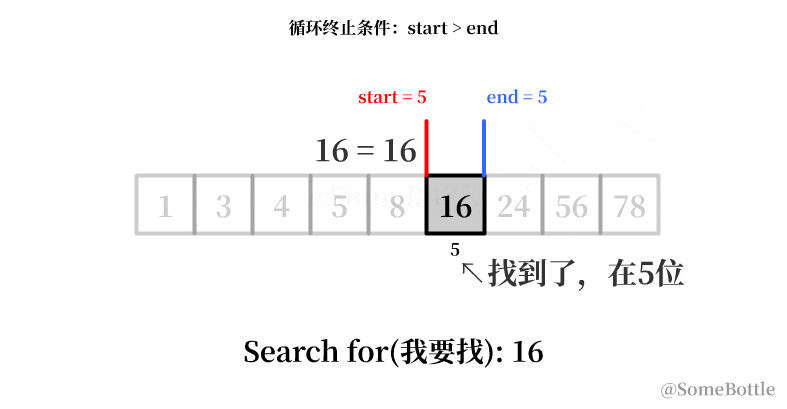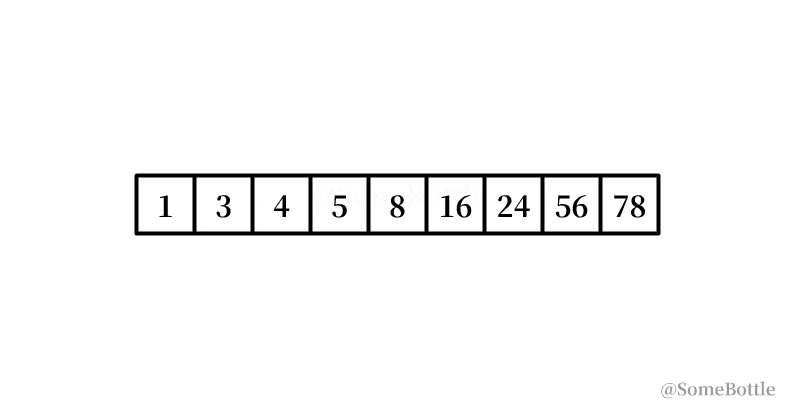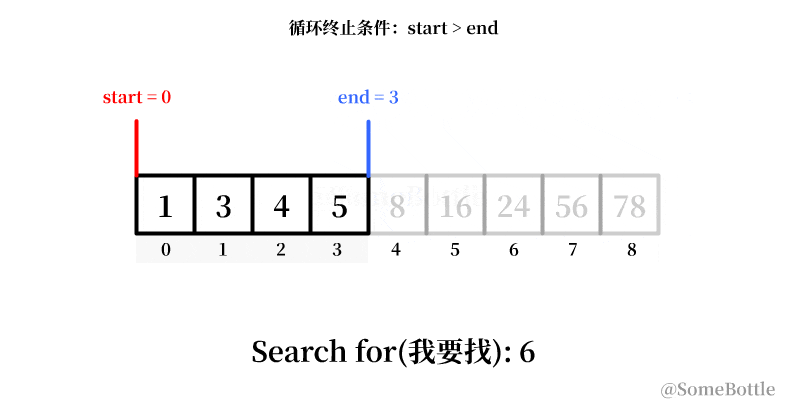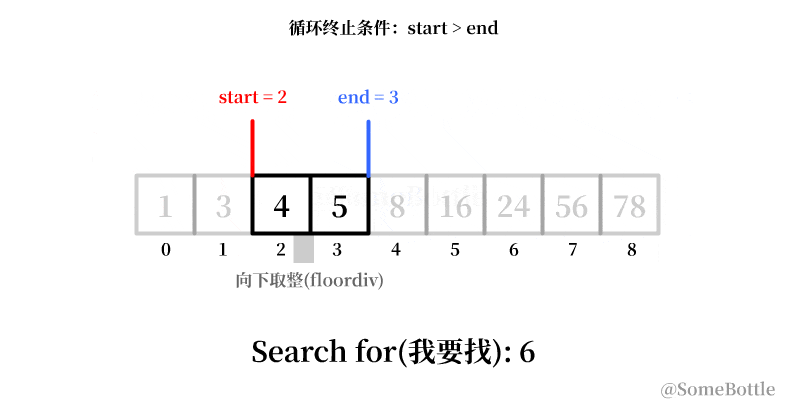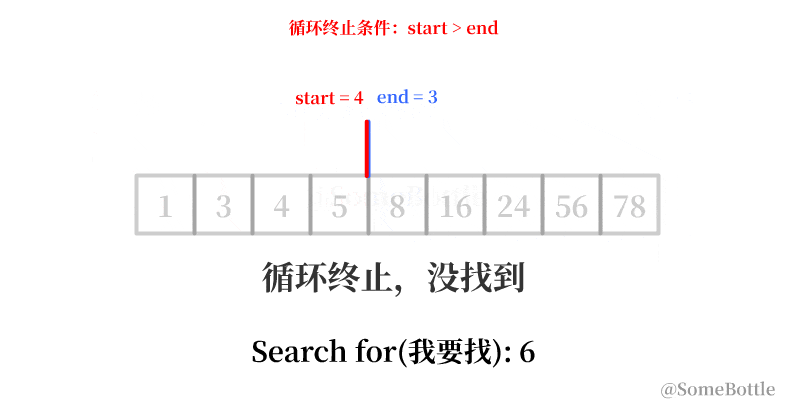进入大二以来一直把学数据结构和算法这事藏在心里,毕竟大学破事太多了,最近实在是按捺不住了。拿起《算法图解》,结合网络上的总结,准备循序渐进入门数据结构和算法...
目前笔记里代码示例我都是用的Python语言(正好学校在教,趁热打铁),日后打C/C++基础后我应该会回来再增加示例。
- 查找的数据目标需要是有顺序的储存结构,比如Python中的列表
list。 - 这个数据目标还需要按一个顺序排列(升序or降序)。
Don't try to understand it.Feel it.
废话不多说了,关于二分查找,我最开始写了个错误的玩意:
# 错误写法例子
my_list = [1, 3, 4, 5, 8, 16, 24, 56, 78]
def find(from_list, which_one):
start = 0
end = len(from_list)-1
while start < end:
middle_ind = (start+end)//2
middle = from_list[middle_ind]
print(start, end)
if middle == which_one:
return middle_ind
elif middle > which_one:
end = middle_ind # 搜索范围尾部前移
elif middle < which_one:
start = middle_ind # 搜索范围头部后移
return False
found_ind = find(my_list, 78)
print(found_ind)这个例子的问题体现在两个方面:
-
一旦寻找的是顺序储存结构中没有的值,会卡在循环里。
-
一旦寻找的是末尾的边缘值,也会卡在循环里。
-
无论是奇数个数据还是偶数个数据都有这个问题。
从输出能看到原因:start和end满足不了end == start的条件,到最后两值会永远差1。
我试着用动画展示一下这个有问题的执行过程:
到最后死循环的时候因为我们将中间值采用了向下取整,导致当start指向倒数第二个索引时卡死在start=7。
通过观察,咱发现每次卡死的时候 start和end永远会相差 1。
很明显了,问题就出现在 每次查找后对start和end的处理 上。就上面这个有问题的代码而言,其实每次搜索后 如果中间项 < 搜索项目,进行start=middle_ind+1的操作就可以,列个表格:
- 搜寻的值:
78
| 搜寻范围 (start,end) | middle_ind (中间项的索引) | start=middle_ind+1 | end | 循环继续 |
|---|---|---|---|---|
| (0,8) | 4 | 5 | 8 | 是 |
| (5,8) | 6 (向下取整) | 7 | 8 | 是 |
| (7,8) | 7 (向下取整) | 8 | 8 | 否 |
↑ 这样的话就能顺利达到查找循环的终止条件start=end了
我的理解:在本次搜索中我们已经检查了middle_ind对应的项目,下一次搜索范围的开始(start)就应该从这一项的下一位开始,也就是middle_ind+1。
但是吧,上面我们找的是末尾的值78,如果找的是开头的值 1 呢?
照葫芦画瓢呗~依照上面的思路,每次搜索后的下一次搜索就应该从这一项的前一位了,也就是middle_ind-1。(上面动画中能直观看出来范围下限索引start是趋于增大的,反之范围上限索引end值就是趋于减小的),再列个表:
- 搜寻的值:
1
| 搜寻范围 (start,end) | middle_ind (中间项的索引) | start | end=middle_ind-1 | 循环继续 |
|---|---|---|---|---|
| (0,8) | 4 | 0 | 3 | 是 |
| (0,3) | 1 (向下取整) | 0 | 0 | 否 |
方便直观对照,我放个静态图在这里:
在寻找既不是开头也不是末尾的值时,搜索过程中往往会交替有start和end的增和减,所以在二分查找程序中关键部分就要兼顾上述两种处理:
if middle == which_one:
return middle_ind
elif middle > which_one:
end = middle_ind-1 # 搜索范围尾部前移,注意是middle_ind-1
elif middle < which_one:
start = middle_ind+1 # 搜索范围头部后移,注意是middle_ind+1(这也是为什么之前寻找列表中没有的值时会卡在循环里)
经过这些处理后,咱成功弥补了这个问题。
等等...在搜索列表中开头或末尾的值时循环在start=end后就停止了...程序仍然无法搜索到开头或末尾的值,而是返回了False!
通过观察发现,其实只要再执行一次循环,问题就完美解决了:把循环条件start < end 换成 start <= end (start等于end时继续循环一次)
最后写成的二分查找代码如下:
def find(from_list, which_one):
start = 0 # 开始的索引
end = len(from_list)-1 # 结尾的索引
while start <= end: # 当范围没有缩减至start>end时,不停二分查找(易错点:为什么用<=?因为当start=end的时候会遗漏一个处理项)
middle_ind = (start+end)//2 # 找到二分中间项目的索引,这里向下取整(floordiv)
middle = from_list[middle_ind] # 获得中间项
if middle == which_one: # 找到了,返回对应的索引
return middle_ind # 找到就停车跑路
elif middle > which_one: # 要寻找的值小于中间值
end = middle_ind-1 # 将范围尾部索引减小到中间值索引-1(易错点)
elif middle < which_one: # 要寻找的值大于中间值
start = middle_ind+1 # 将范围头部索引start增大到中间值索引+1(易错点)
return False # 啥都没找到最后咱基于上面的写法整了几个动画:
-
寻找列表最开头的值:
my_list = [1, 3, 4, 5, 8, 16, 24, 56, 78] found_ind = find(my_list, 1) # 0
-
寻找列表中间的一个值:
my_list = [1, 3, 4, 5, 8, 16, 24, 56, 78] found_ind = find(my_list, 16) # 5
-
寻找一个找不到的值:
my_list = [1, 3, 4, 5, 8, 16, 24, 56, 78] found_ind = find(my_list, 6) # False
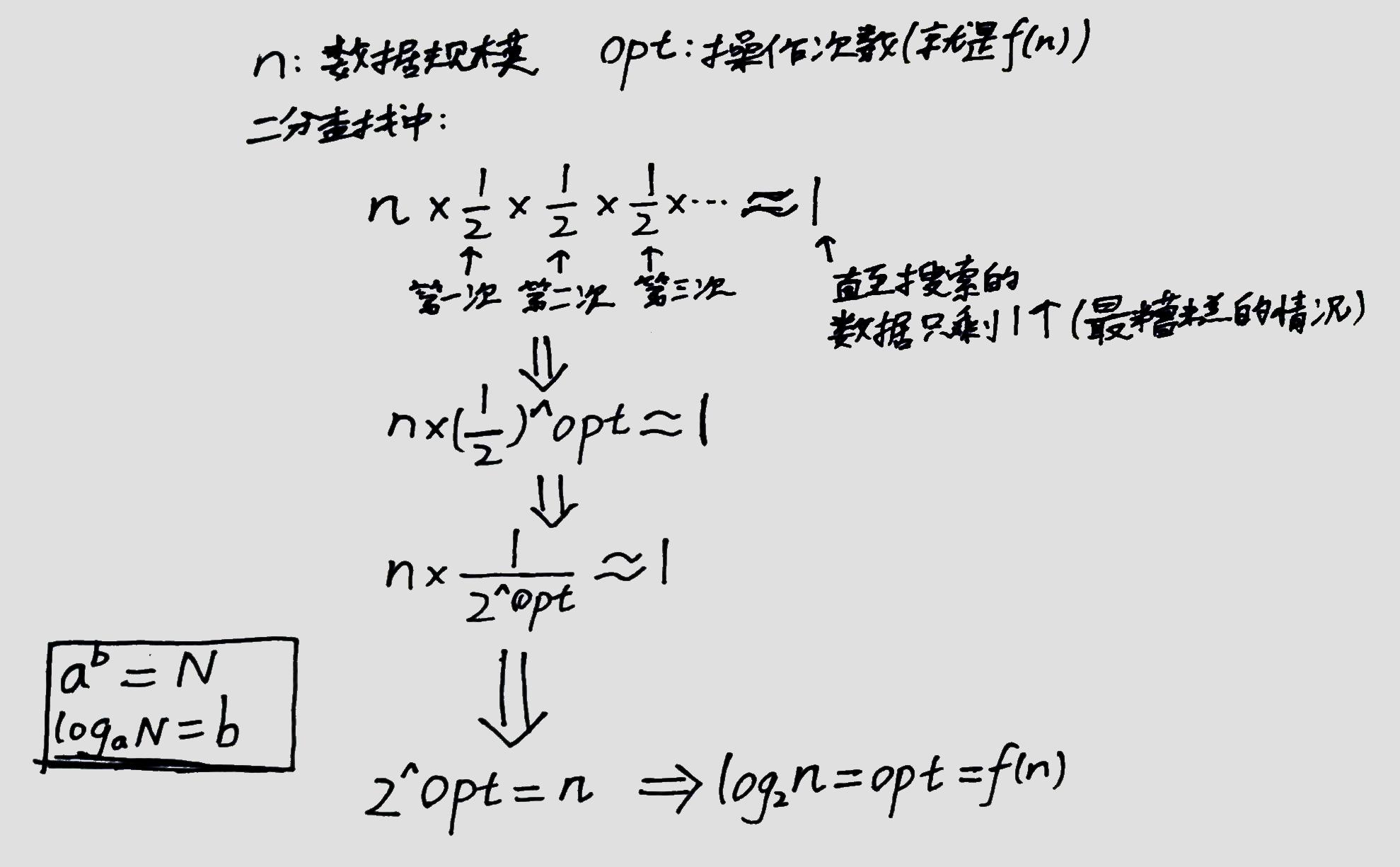
通过大O表示法咱可以写成 O(f(n)) 这样,其中:
n是操作的数据的规模。f(n)是操作的次数(程序执行的次数)。- 大O的量和
f(n)成正比(这是不是说明看O其实就可以粗略地看f(n)?)。
上面例子的列表中有9个元素,数据规模 n=9,这些例子中除了卡死循环的情况外,我发现程序 最多 执行检查4次,而不是9次——
——因为每次执行操作后会将搜索范围折半,也就是每次操作后数据规模会成半缩减:
(字丑勿cue ┑( ̄Д  ̄)┍)
所以二分查找的时间复杂度表示为 O(log2n)。
为什么说到“最多”这个词呢?因为大O时间体现的是最不理想情况下的运行时间,也就是该算法的时间复杂度的上界。
这篇笔记里的二分查找写法只是所有写法中的一种。我认为掌握一个算法并不是要对每种写法都了如指掌,而是要去理解其中的原理。
这里贴个知乎问题贴:
注意这个链接里的回答说 median = ( low + high ) / 2 写法会溢出是 C/C++ 里的一个小坑。