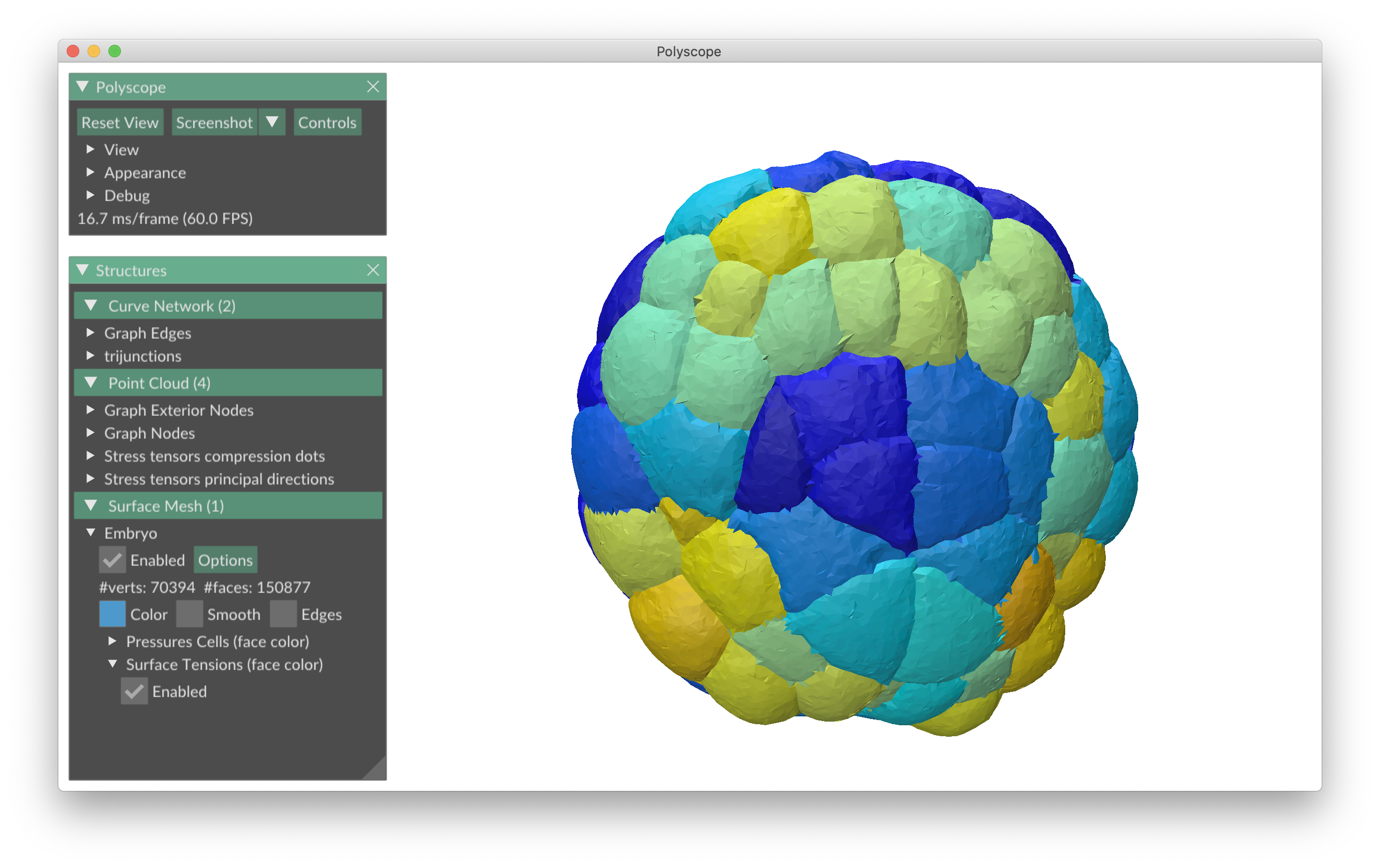
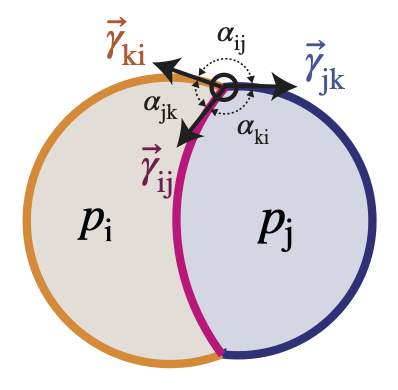
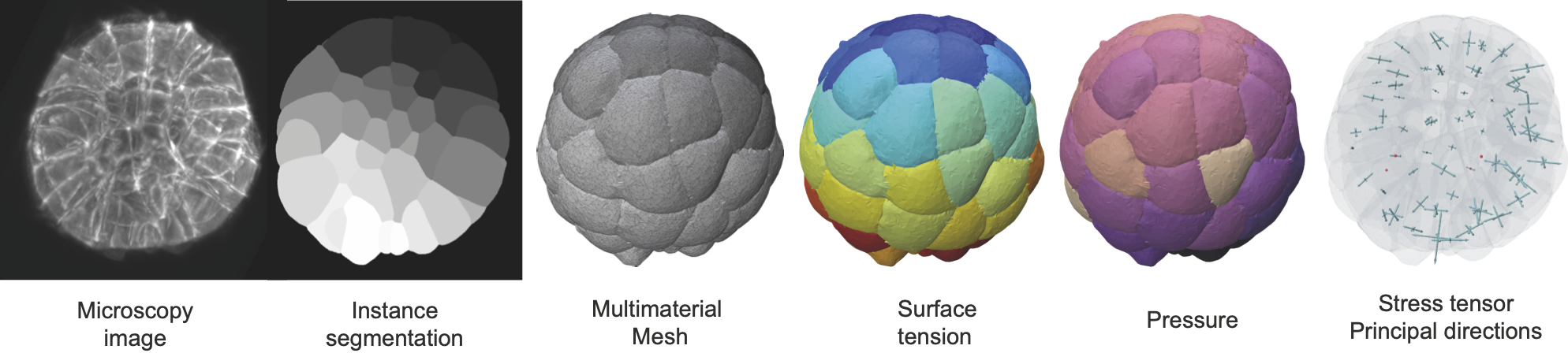
foambryo is a python package developed to infer relative surface tensions and cell pressures from the 3D geometry of cells in foam-like clusters, such as early-embryos, tissues or organoids.
It was developed by Sacha Ichbiah during his PhD in Turlier Lab, and is maintained by Matthieu Perez and Hervé Turlier. For support, please open an issue. If you use our library in your work please cite the paper.
If you are interested in inferring tensions in 2D, please look at the foambryo2D package instead.
Multicellular structures encountered in the field of developmental biology have various shapes and arrangements that reflectes their physiological functions. Mechanics is at the heart of the development of these structures, yet tools to investigate the forces at play in 3D remain scarse. Inferring forces or stresses from cell shapes only allows one to reveal the fundamental mechanics shaping cells from microscopy imaging. This software makes the hypothesis that cells in many early embryos, tissues and cell aggregates are mechanically akin to heterogeneous foam-like structures (see Physical model).
foambryo requires Python >3.6 with pip.
foambryo requires the prior segmentation of images of multicellular aggregates into cell segmentation masks using one's favorite algorithm (watershed algorithm, cellpose or any preferred one). The quality of the segmentation and the size of the original image will directly affect the precision of the inference results.
All required dependencies are installed by pip automatically.
foambryo relies on a companion tool delaunay-watershed that we developed to construct precise multimaterial meshes from instance segmentations. From these multimaterial meshes, one can efficiently and robustly measure junction angles and interface curvatures to invert the Young-Dupré and Laplace laws and infer the surface tensions
The viewer is based on Polyscope, a C++/Python viewer designed to visualize 3-dimensional geometry, in particular meshes.
This package should work on any OS and was tested on the following macOS and Linux systems:
macOS: BigSur (11.7.9) and Ventura (13.5)
Linux: Ubuntu 16.04, CentOS 7 and Manjaro 22.0
We recommend to install foambryo from the PyPI repository directly.
pip install foambryoTo use the foambryo viewers, use instead:
pip install "foambryo[viewing]"For developers, you may also install foambryo by cloning the source code and installing from the local directory.
First, make sure you have the LFS git extension, as there are some large data alongside the source code, necessary to run the example notebook.
git clone https://github.com/VirtualEmbryo/foambryo.git
pip install pathtopackage/foambryoLoad an instance segmentation, reconstruct its multimaterial mesh, infer and visualize the forces with Polyscope
from foambryo import dcel_mesh_from_segmentation_mask
from foambryo.viewing import plot_force_inference, plot_tension_inference
# Load the labels
import skimage.io as io
segmentation = io.imread("Segmentation.tif")
# Reconstruct a multimaterial mesh from segmentation
mesh = dcel_mesh_from_segmentation_mask(segmentation_mask) # DCEL mesh ready for force inference !
# Infer and view the forces
plot_force_inference(mesh)
#Or just the tensions
plot_tension_inference(mesh)See the introductory notebook for further details.
We consider a tissue constituted of cells i.
They minimize, under conservation of volume an energy
The two main laws underlying mechanical force balance are:
-
Young-Dupré Law:
$\gamma_{ij} + \gamma_{ik} + \gamma_{jk} = 0$ . -
Laplace Law:
$p_j - p_i = 2 \gamma_{ij} H_{ij}$ where$H_{ij}$ is the mean curvature of the interface between the cell i and j.
See the introductory notebook to understand the API.
The notebook shows how to create a mesh and how foambryo compute forces on the mesh.
We recall that the forces are relative, this is why you need to give the mean tension and base pressure.
base_pressure: reference exterior pressure. All pressures inside cells are computed relative to this one.mean_tension: as one only infers ratios between tensions, it has to be given. You can set it to 1 for instance.
Foambryo has several strategies to compute tensions:
YoungDupre(Young-Dupré with cosines only),ProjectionYoungDupre(Young-Dupré with cosines and sines),Equilibrium,Cotan(cotangent formula, see Yamamoto et al. 2023),InvCotan(inverse of the cotangent formula),Lami(Lami's theorem),InvLami(inverse of the Lami's relation),LogLami(logarithm of the Lami's relation),Variational(variational formulation, see our paper).
And also to compute pressures:
Variational(variational formulation, see our paper),Laplace(Laplace's law)WeightedLaplace(Laplace's law with weight on curvature by area).
Phallusia mammillata is a solitary marine tunicate of the ascidian class known for its stereotypical development. As the embryo develops freely, without any constraint, we can do a full force inference and infer its tensions, pressures and stresses. We use segmentation data from Guignard, L., Fiúza, U. et al.
Caenorhabditis elegans is a widely studied model organism, with one of the most reproducible development. The embryo of this earthworm is developing within a shell. As the shell shape and mechanics is unknown, the pressures are not accessible. However we can still use Young-Dupré relationships to retrieve surface tensions at cell membranes. Here we use segmentation data from Cao, J., Guan, G., Ho, V.W.S. et al.
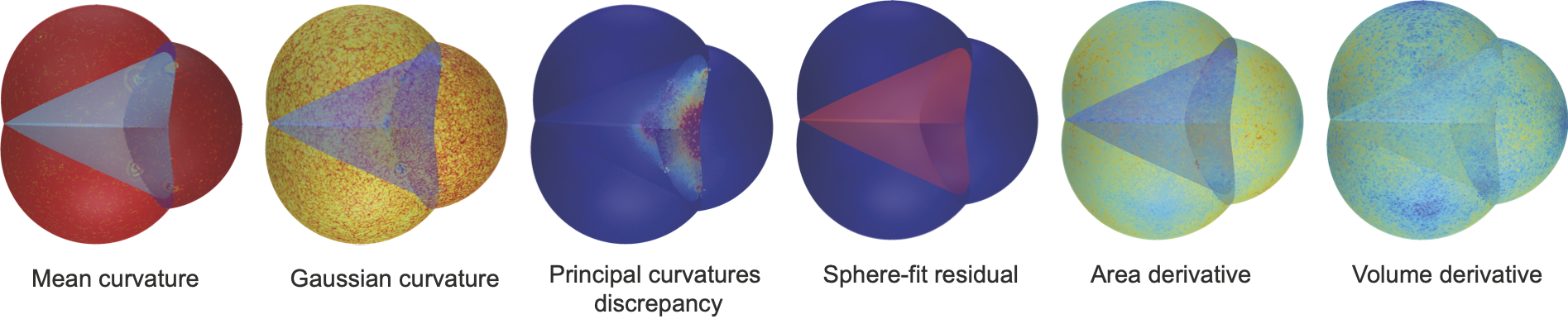
Gaussian and mean curvatures can be plotted on our meshes, and may be useful to study the geometric properties of interfaces between cells.
We can also plot the vertex area and volume derivatives, that appear in our variational formulas, the difference between the two principal curvatures and the residual of the best sphere-fit that can be used to detect non-spherical constant-mean-curvature surfaces.
They can be obtained by putting the option scalar_quantities = True when viewing the forces.
- Gaussian Curvature is computed using the angle defect formula.
- Mean Curvature is computed using the cotan formula.
To see the code of each of these use-cases, please load the associated jupyter notebooks in the folder Notebooks
If you use this tool, please cite the associated preprint: Do not hesitate to contact Matthieu Perez and Hervé Turlier for practical questions and applications. We hope that foambryo could help biologists and physicists to shed light on the mechanical aspects of early development.
@article {Ichbiah2023.04.12.536641,
author = {Sacha Ichbiah and Fabrice Delbary and Alex McDougall and R{\'e}mi Dumollard and Herv{\'e} Turlier},
title = {Embryo mechanics cartography: inference of 3D force atlases from fluorescence microscopy},
elocation-id = {2023.04.12.536641},
year = {2023},
doi = {10.1101/2023.04.12.536641},
publisher = {Cold Spring Harbor Laboratory},
abstract = {The morphogenesis of tissues and embryos results from a tight interplay between gene expression, biochemical signaling and mechanics. Although sequencing methods allow the generation of cell-resolved spatio-temporal maps of gene expression in developing tissues, creating similar maps of cell mechanics in 3D has remained a real challenge. Exploiting the foam-like geometry of cells in embryos, we propose a robust end-to-end computational method to infer spatiotemporal atlases of cellular forces from fluorescence microscopy images of cell membranes. Our method generates precise 3D meshes of cell geometry and successively predicts relative cell surface tensions and pressures in the tissue. We validate it with 3D active foam simulations, study its noise sensitivity, and prove its biological relevance in mouse, ascidian and C. elegans embryos. 3D inference allows us to recover mechanical features identified previously, but also predicts new ones, unveiling potential new insights on the spatiotemporal regulation of cell mechanics in early embryos. Our code is freely available and paves the way for unraveling the unknown mechanochemical feedbacks that control embryo and tissue morphogenesis.Competing Interest StatementThe authors have declared no competing interest.},
URL = {https://www.biorxiv.org/content/early/2023/04/13/2023.04.12.536641},
eprint = {https://www.biorxiv.org/content/early/2023/04/13/2023.04.12.536641.full.pdf},
journal = {bioRxiv}
}
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.