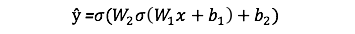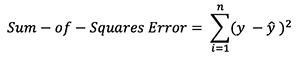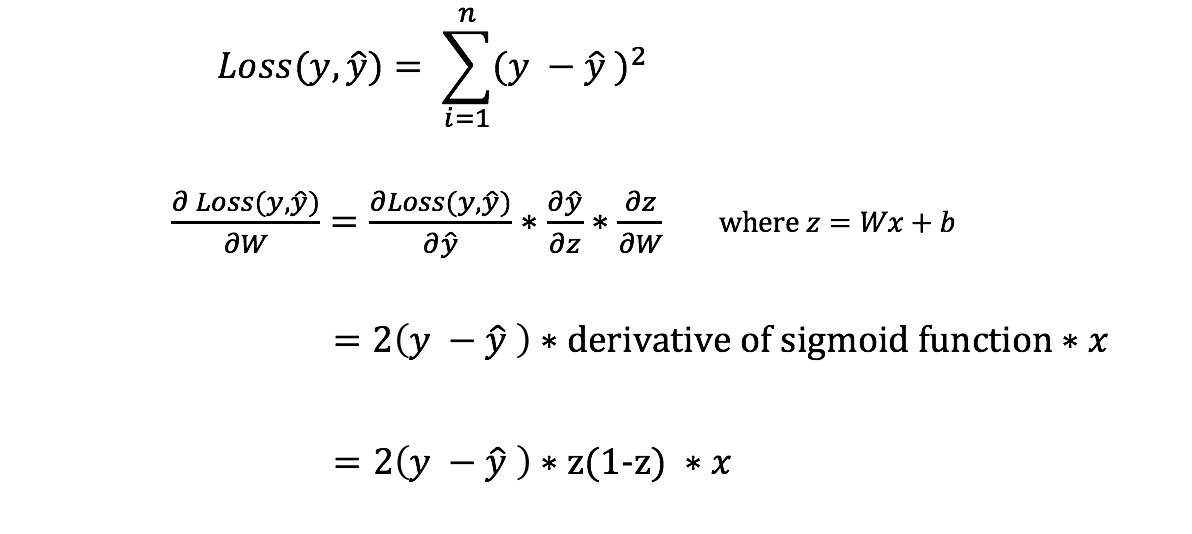"Neural Networks", we mean artificial Neural Networks (ANN). The idea of ANN is based on biological neural networks like the brain. The basic structure of a neural network is the neuron. Similarly the ANN has as perceptron/neuron ,its a simulation of human body neuron.
-
The perceptron functions basically on a concept of activation function.
-
Unless the result is greater than a certain threshold there won't be any putput with respect to the perceptron.
As one can see in this formula, the output will be one unless the value exceeds the threshold function.
Objective: Try to make a perceptron learn how the weights and values vary as for the AND and OR gates.
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
For this gate, the perceptron will receive Input1 and Input2 and weights need to be assinged to the Inputs respectively.
For this case lets say threshold is 1. Hence as per the activation fucntion the cumulative value (w1x1+w2x2) should be greater than the threshold in the last case only. Hence you can say that possible values will be w1=0.6 w2=0.6
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
For this gate, the perceptron will receive Input1 and Input2 and weights need to be assinged to the Inputs respectively.
For this case lets say threshold is 0.5. Hence as per the activation fucntion the cumulative value (w1x1+w2x2) should be greater than the threshold in the last three cases only. Hence you can say that possible values will be w1=0.6 w2=0.6
Here comes the concept of feed foward and back propagation. Those are huamn relatable analogies for a learning something.
import numpy as np
#Constructing AND and OR Gate as per the logic weights
class Perceptron:
def __init__(self,input_lengths,weights="None"):
if weights is None:
self.weights =np.ones(input_lengths)*0.5
else:
self.weights=weights
@staticmethod
def unit_step_function(x):
if x>0.3: # Defining Threshold for the neuron 0.3 for OR gate and will be 0.5 for AND gate
return 1
return 0
def __call__(self,in_data):
weighted_input=self.weights*in_data
weighted_sum=weighted_input.sum()
return Perceptron.unit_step_function(weighted_sum)
Here is the perceptron for the Gate logic: Trials and results
Implementing for AND Gate
p = Perceptron(2, np.array([0.5, 0.5]))#Change the weights here
for x in [np.array([0, 0]), np.array([0, 1]),
np.array([1, 0]), np.array([1, 1])]:
y = p(np.array(x))
print(x, y)
Pushing the inputs:
p = Perceptron(2, np.array([0.5, 0.5]))#Change the weights here
for x in [np.array([0, 0]), np.array([0, 1]),
np.array([1, 0]), np.array([1, 1])]:
y = p(np.array(x))
print(x, y)
Here is the perceptron for the Gate logic: Trials and results
OR Gate
Results:
Inputs Outputs
[0 0] 0
[0 1] 0
[1 0] 0
[1 1] 1
AND Gate
Results:
Inputs Outputs
[0 0] 0
[0 1] 1
[1 0] 1
[1 1] 1
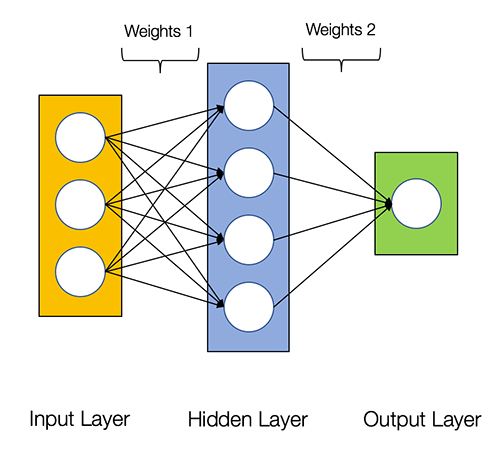
Neural Networks consist of the following components
-
An input layer, x
-
An arbitrary amount of hidden layers
-
An output layer, ŷ
-
A set of weights and biases between each layer, W and b
-
A choice of activation function for each hidden layer, σ.
The diagram below shows the architecture of a 2-layer Neural Network (note that the input layer is typically excluded when counting the number of layers in a Neural Network)
A sample code to implement two layer network:
class NeuralNetwork:
def __init__(self, x, y):
self.input = x
self.weights1 = np.random.rand(self.input.shape[1],4)
self.weights2 = np.random.rand(4,1)
self.y = y
self.output = np.zeros(y.shape)
The output ŷ of a simple 2-layer Neural Network is:
You might notice that in the equation above, the weights W and the biases b are the only variables that affects the output ŷ.
Naturally, the right values for the weights and biases determines the strength of the predictions. The process of fine-tuning the weights and biases from the input data is known as training the Neural Network.
Each iteration of the training process consists of the following steps:
Calculating the predicted output ŷ, known as feedforward Updating the weights and biases, known as backpropagation The sequential graph below illustrates the process.
In a feed forward network information always moves one direction; it never goes backwards.
A feedforward neural network is an artificial neural network wherein connections between the nodes do not form a cycle.
The feedforward neural network was the first and simplest type of artificial neural network devised.
Backpropagation is a method used in artificial neural networks to calculate a gradient that is needed in the calculation of the weights to be used in the network.
Backpropagation is shorthand for "the backward propagation of errors," since an error is computed at the output and distributed backwards throughout the network’s layers.
It is commonly used to train deep neural networks,[3] a term referring to neural networks with more than one hidden layer.
However, we still need a way to evaluate the “goodness” of our predictions (i.e. how far off are our predictions)? The Loss Function allows us to do exactly that.
There are many available loss functions, and the nature of our problem should dictate our choice of loss function.
Simple Example: sum-of-sqaures error as our loss function.
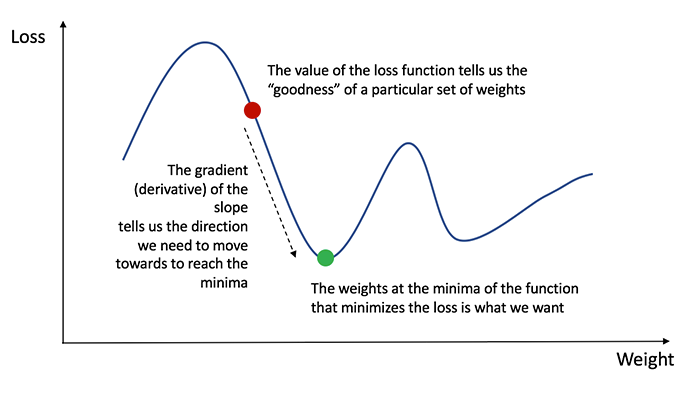
In order to know the appropriate amount to adjust the weights and biases by, we need to know the derivative of the loss function with respect to the weights and biases.
If we have the derivative, we can simply update the weights and biases by increasing/reducing with it(refer to the diagram above). This is known as gradient descent.
However, we can’t directly calculate the derivative of the loss function with respect to the weights and biases because the equation of the loss function does not contain the weights and biases. Therefore, we need the chain rule to help us calculate it.